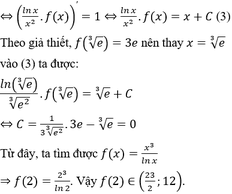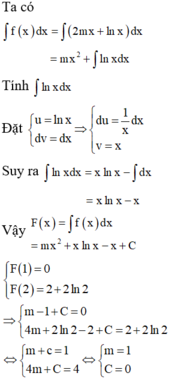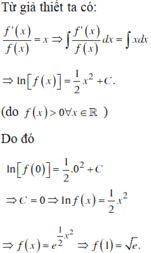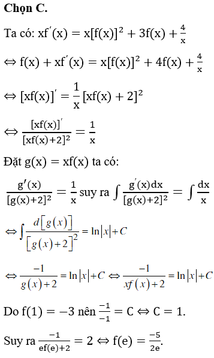Cho hàm số f(x) thỏa mãn: xf'(x).lnx + f(x) = 2x2, ∀x ∈ (1;+∞) và f(e) = e2. Tính tích phân I=\(\int\limits^{e^2}_e\dfrac{x}{f\left(x\right)}dx\)

Những câu hỏi liên quan
Cho hàm số yf(x) có đạo hàm liên tục trên (1;+∞) và thỏa mãn
x
f
(
x
)
-
2
f
(
x
)
.
l
n
x
x
3
-
f
(
x
)
,∀x∈(1;+∞); biết
f
(...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên (1;+∞) và thỏa mãn x f ' ( x ) - 2 f ( x ) . l n x = x 3 - f ( x ) ,∀x∈(1;+∞); biết f ( e 3 ) = 3 e . Giá trị f(2) thuộc khoảng nào dưới đây
A. ( 12 ; 25 / 2 )
B. ( 13 ; 27 / 2 )
C. ( 23 / 2 ; 12 )
D. ( 14 ; 29 / 2 )
Cho hàm số f(x) thỏa mãn f'(x) + 2x.f(x) = f(x).lnx với f(x)≠ 0, ∀x và f(1) =1. Khi đó \(\left|f\left(2\right)\right|\) bằng ?
\(\Leftrightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}+2x=lnx\Rightarrow\dfrac{f'\left(x\right)}{f\left(x\right)}=lnx-2x\)
Lấy nguyên hàm 2 vế:
\(\Rightarrow\int\dfrac{f'\left(x\right)}{f\left(x\right)}dx=\int\left(lnx-2x\right)dx\)
\(\Rightarrow ln\left|f\left(x\right)\right|=x\left(lnx-1\right)-x^2+C\)
Thay \(x=1\)
\(\Rightarrow ln\left|f\left(1\right)\right|=-2+C\Rightarrow C=2\)
\(\Rightarrow ln\left|f\left(x\right)\right|=x\left(lnx-1\right)-x^2+2\)
\(\Rightarrow\left|f\left(x\right)\right|=e^{x\left(lnx-1\right)-x^2+2}\)
\(\Rightarrow\left|f\left(2\right)\right|\)
Đúng 2
Bình luận (0)
Cho hàm số f(x) 2mx + lnx. Tìm m để nguyên âm F(x) của f(x) thỏa mãn F(1) 0 và F(2) 2 +2ln2
Đọc tiếp
Cho hàm số f(x) = 2mx + lnx. Tìm m để nguyên âm F(x) của f(x) thỏa mãn F(1) = 0 và F(2) = 2 +2ln2
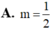
![]()
![]()
![]()
Một nguyên hàm F(x) của hàm số
f
(
x
)
ln
x
+
x
2
+
1
thỏa mãn F(0) 1. Chọn kết quả đúng
Đọc tiếp
Một nguyên hàm F(x) của hàm số f ( x ) = ln x + x 2 + 1 thỏa mãn F(0) = 1. Chọn kết quả đúng
![]()
![]()
![]()
![]()
Chọn A.
Đặt u = ln x + x 2 + 1 , d v = d x ta được
F(x)=x ln x + x 2 + 1 - x 2 + 1 + C
Vì F(0) = 1 nên C = 2
Vậy ![]()
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm dương trên [1;2] thỏa mãn
f
(
1
)
1
e
và
x
f
(
x
)
+
(
x
+
1
)
f
(
x
)
3
x
2
e
-
x
. Tính f(2) A.
f
(...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm dương trên [1;2] thỏa mãn f ( 1 ) = 1 e và x f ' ( x ) + ( x + 1 ) f ( x ) = 3 x 2 e - x . Tính f(2)
A. f ( 2 ) = 1 e 2
B. f ( 2 ) = 2 e 2
C. f ( 2 ) = 4 e 2
D. f ( 2 ) = 8 e 2
Cho hàm số yf(x) có đạo hàm liên tục trên R thỏa mãn
x
f
(
x
)
.
f
(
x
)
f
2
(
x
)
-
x
,
∀
x
∈
ℝ
và f(2)1 .Tích phân bằng A.
3
2
B.
4
3
C. 2 D....
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R thỏa mãn x f ( x ) . f ' ( x ) = f 2 ( x ) - x , ∀ x ∈ ℝ và f(2)=1 .Tích phân bằng
A. 3 2
B. 4 3
C. 2
D. 4
Chọn đáp án C.
Lấy tích phân hai vế trên đoạn [0;2] có
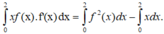
Tích phân từng phần có
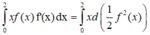
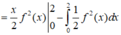
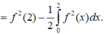
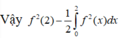
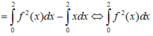
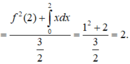
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm liên tục trên
ℝ
thỏa mãn f(x) -xf(x) 0,
f
x
0
,
∀
x
∈
ℝ
và f(0) 1. Giá trị của f(1) bằng? A.
1
e
. B.
1
e
.
C.
e
.
D. e.
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên ℝ thỏa mãn f'(x) -xf(x) = 0, f x > 0 , ∀ x ∈ ℝ và f(0) = 1. Giá trị của f(1) bằng?
A. 1 e .
B. 1 e .
C. e .
D. e.
Cho hàm số yf(x) xác định và liên tục trên [1;e] thỏa mãn
xf
(
x
)
x
[
f
(
x
)
]
2
+
3
f
(
x
)
+
4
x
và f(1) -3. Tính f(e). A.
5
2
e
B. -...
Đọc tiếp
Cho hàm số y=f(x) xác định và liên tục trên [1;e] thỏa mãn xf ' ( x ) = x [ f ( x ) ] 2 + 3 f ( x ) + 4 x và f(1) = -3. Tính f(e).
A. 5 2 e
B. - 5 2
C. - 5 2 e
D. 5 2
Biết F(x) là một nguyên hàm của hàm số f(x) x3 – 2x2 + 3 thỏa mãn F(1) 3. Khi đó F(x) bằng A.
x
4
4
-
2
x
3
3
+
3
x
+
5
12
B. ...
Đọc tiếp
Biết F(x) là một nguyên hàm của hàm số f(x) = x3 – 2x2 + 3 thỏa mãn F(1) = 3. Khi đó F(x) bằng
A. x 4 4 - 2 x 3 3 + 3 x + 5 12
B. x 4 4 - 2 x 3 3 + 3 x + 7 12
C. x 4 4 - 2 x 3 3 + 3 x + 1 12
D. 3 x 2 - 4 x + 4