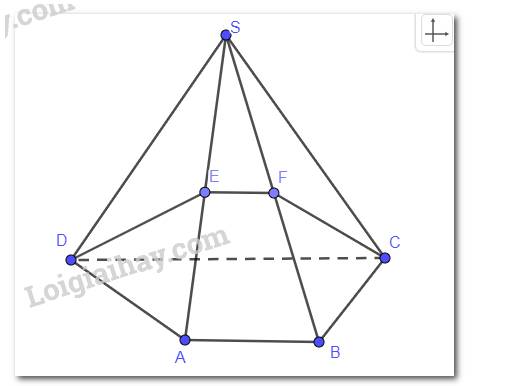
cho hình chóp S.ABCD có đáy tứ giác ABCD sao cho \(AB\cap CD=E\) ; \(AC\cap BD=F\)
a) Xác định giao tuyến (SAB) và (SCD); (SAC) và (SBD)
b) Xác định giao tuyến mp (SEF) với (SAD); (SBC)
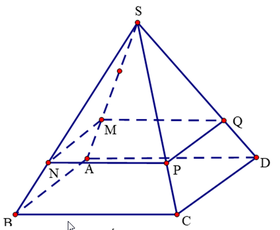
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp S.ABCD cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB,CD để thiết diện đó là hình bình hành?
A. AB = 3CD
B. AB = 2CD
C. CD = 2AB
D. CD = 3AB
Đáp án A
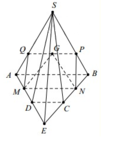
Qua G kẻ đường thẳng d song song với AB và cắt SA, SB lần lượt tại hai điểm Q, P. Vì MN là đường trung bình của ABCD ⇒ MN//AB
Do đó MN//PQ. Vậy giao tuyến của mặt phẳng (MNG) và (SAB) là PQ.
Mặt phẳng (MNG) cắt khối chóp S.ABCD theo thiết diện là tứ giác MNPQ
Vì MN//PQ suy ra MNPQ là hình thang
Để MNPQ là hình bình hành ⇔ MN=PQ (1)
Gọi I là trung điểm của AB, G là trọng tâm tam giác S A B ⇒ S G S I = 2 3
Tam giác SAB có P Q / / A B ⇒ P Q A B = S G S I = 2 3 ⇔ P Q = 2 3 A B (2)
Mà MN là đường trung bình hình thang A B C D ⇒ M N = A B + C D 2 (3)
Từ (1) , (2) và (3) suy ra 2 3 A B = A B + C D 2 ⇔ 4 A B = 3 A B + 3 C D ⇔ A B = 3 C D .
Bài 5. Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh a. Mặt bên hợp với đáy một góc . Tính VS ABCD . theo a và . Bài 6. Tính thể tích khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a và góc ASB = α . Áp dụng: Tính VS ABCD . trong trường hợp α = 60 độ.
Bài 7. Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc ABC =120độ . Cho SA vuông góc với đáy và SC = 2a .Tính thể tích hình chóp S.ABCD.
Bài 8. Cho hình chóp S.ABCD có đáy ABCD là một hình thang cân (AB//CD) với AC=20 cm BC=15 cm AB=25 cm . Cho SA vuông góc với đáy và SA =18cm . Tính thể tích của khối chóp.
Bài 9. Cho hình chóp S.ABC có SA vuông góc với đáy. Mặt bên SBC là tam giác đều cạnh a. Cho gócBAC =120 . Tính VS ABC .
. Bài 10. Cho khối chóp S.ABC có đường cao SA bằng a, đáy là tam giác vuông cân có AB= BC= a . Gọi B' là trung điểm của SB, C' là chân đường cao hạ từ A của tam giác S.ABC:
a.Tính thể tích khối chóp S.ABC
b.Chứng minh SC vuông góc với (AB'C')
c.Tính thể tích khối chóp S.ABC
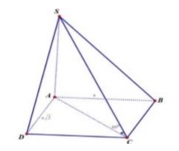
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật có các cạnh A B = a , A D = a 2 , S A ⊥ A B C D , góc giữa SC và đáy bằng 60 ° . Thể tích hình chóp S.ABCD bằng
A. 2 a 3
B. 3 2 a 3
C. a 3
D. 6 a 3
Đáp án A
Ta có A ⇔ = a 2 + a 2 2 = a 3
S
A
=
A
C
tan
60
0
=
a
3
.
3
=
3
a
;
S
A
B
C
D
a
.
a
2
=
a
2
2
Thể tích hình chóp S.ABCD là:
V = 1 3 S A . S B A C D = 1 3 .3 a . a 2 2 = a 3 2
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhất AB = a , A D = a 2 , S A ⊥ A B C D góc tích của giữa SC và đáy bằng 60 ° Thểkhối chóp S.ABCD bằng:
A. 3 2 a 3
B. 6 a 3
C. 3 a 3
D. 2 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình thang có cạnh đáy AB và CD. Gọi M, N lần lượt là trung điểm của các cạnh AD, BC. G là trọng tâm của tam giác SAB. Thiết diện của hình chóp ![]() cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?
cắt bởi (IJG) là một tứ giác. Tìm điều kiện của AB, CD để thiết diện đó là hình bình hành?

A. AB=3CD
B. AB=2CD
C. CD=2AB
D. CD=3AB
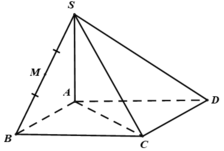
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật cạnh AB = a, AD = a 2 , SA⊥(ABCD) góc giữa SC và đáy bằng 60°. Thể tích hình chóp S.ABCD bằng:
A. a 3 2
B. 3 a 3 2
C. 3 a 3
D. a 3 6
Đáp án A
Theo bài ra ta có:
SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD). Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng tứ giác MNCD là hình thang.
Xét tam giác SAB ta có MN là đường trung bình suy ra MN // AB.
Mà AB // CD do đó MN // CD.
Suy ra MNCD là hình thang.
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 10. Gọi M là điểm trên SA sao cho S M S A = 2 3 . Một mặt phẳng (α) đi qua M song song với AB và CD, cắt hình chóp theo một tứ giác có diện tích là:
A. 400 9 .
B. 16 9 .
C. 4 9 .
D. 20 3 .
Đáp án A
Qua M dựng đường thắng song song AB cắt SB tại N.
Qua M dựng đường thắng song song AD cắt SD tại Q.
Qua N dựng đường thắng song song BC cắt SC tại P.
Ta có M N // A B ⇒ M N // A B C D N P // B C ⇒ N P // A B C D .
⇒ M N P Q / / A B C D .
Tương tự câu 1 ta có tỉ lệ diện tích S M N P Q S A B C D = M N A B 2 = S M S A 2 = 4 9 .
Ta có S A B C D = 10.10 = 100 ⇔ S M N P Q = 100. 4 9 = 400 9
Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhất AB = a, AD=a 2 , SA ⊥ (ABCD) góc giữa SC và đáy bằng 60 o . Thể tích của khối chóp S.ABCD bằng:
A. 3 2 a 3
B. 6 a 3
C. 3 a 3
D. 2 a 3
Chọn D.
Theo giả thiết góc giữa SC và đáy bằng 60 o suy ra S C A ^ = 60 o
ABCD là hình chữ nhật nên A C = A B 2 + B C 2 = a 3
Tam giác SAC vuông tại A nên S A = A C . tan 60 o = 3 a
Diện tích đáy là S A B C D = A B . A D = 2 a 2
Thể tích khối chóp S.ABCD là V = 1 3 2 a 2 . 3 a = 2 a 3
Cho hình chóp tứ giác đều S.ABCD có đáy ABCD là hình vuông cạnh AB = a (a>0) Góc giữa mặt bên và mặt đáy bằng 60 ° Tính thể tích khối chóp S.ABCD:
A. a 3 3 2
B. a 3 6
C. a 3 3 3
D. a 3 3 6