Cho hình thang cân \(ABCD\), đáy lớn \(CD = 5\), \(\widehat{A\text{D}C}=30^o\), \(DA=\sqrt{3}\); \(\overrightarrow{DB}=x\overrightarrow{DA}+y\overrightarrow{DC}\). Tính giá trị của \(x+y\).

Những câu hỏi liên quan
Cho hình thang cân ABCD (AB // CD) có \(\widehat{A}=\widehat{B}=60^o\); AB= 4,5 cm; AD = BC = 2cm. Tính độ dài đáy CD và diện tích hình thang cân ABCD.
cho hình thang vuông ABCD\(\left(\widehat{A}=\widehat{D}=90^0\right)\)có đáy nhỏ AB=5cm, đáy lớn CD =9cm; góc tạo bởi đáy lớn và cạnh bên là 45o. Tính chu chu vi hình thang vuông ABCD
Kẻ \(BH\perp CD\)
Mà \(CD\perp AD\left(gt\right)\Rightarrow BH//AD\)
Hình thang ABHD (AB//HD) có BH//AD nên \(\hept{\begin{cases}HD=AB=5\left(cm\right)\\BH=AD\end{cases}}\) (t/c hình thang)
\(HD+HC=DC\Rightarrow5+HC=9\Rightarrow HC=4\left(cm\right)\)
\(\Delta HBC\)vuông cân tại H nên \(HB=HC=4cm\Rightarrow AD=4cm\left(AD=BH\right)\)
Áp dụng định lí Pitago tính được \(BC=\sqrt{32}\left(cm\right)\)
Chu vi hình thang vuông ABCD là:
\(AB+BC+CD+AD=5+\sqrt{32}+9+4=18+\sqrt{32}\left(cm\right)\)
Chúc bạn học tốt.
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có đáy nhỏ AB1, đáy lớn CD3, cạnh bên
B
C
D
A
2
. Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng: A.
4
3
π
. B.
5
3
π
. C.
2
3
π...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB=1, đáy lớn CD=3, cạnh bên B C = D A = 2 . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng:
A. 4 3 π .
B. 5 3 π .
C. 2 3 π .
D. 7 3 π .
Đáp án D
Ta có: A E = B F = 1
Khi đó: D E = A D 2 − A E 2 = 1
Khi quay hình chữ nhật DEFC quanh trục AB ta được hình trụ có thể tích là:
V 1 = π D E 2 . D C = π .1 2 .3 = 3 π
Khi quay tam giác AED quanh trục AB ta được hình nón có thể tích là:
V 2 = 1 3 π D E 2 . A E = 1 3 π .1 2 .1 = π 3
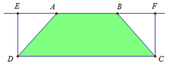
Do đó thể tích vận tròn xoay tạo thành khi cho hình thang quay quanh AB là:
V = V 1 − 2 V 2 = 7 π 3
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có đáy nhỏ
A
B
1
; đáy lớn
C
D
3
, cạnh bên
B
C
D
A
2
. Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng A.
4
3
π
B.
5
3
π
C.
2
3
π...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ A B = 1 ; đáy lớn C D = 3 , cạnh bên B C = D A = 2 . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng
A. 4 3 π
B. 5 3 π
C. 2 3 π
D. 7 3 π
Cho hình thang cân ABCD có đáy nhỏ AB 1 đáy lớn CD 3, cạnh bên
B
C
D
A
2
. Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng A.
5
3
π
B.
4
3...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ AB =1 đáy lớn CD =3, cạnh bên B C = D A = 2 . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng
A. 5 3 π
B. 4 3 π
C. 7 3 π
D. 2 3 π
Chọn đáp án C
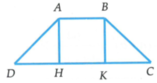
Gọi H, K lần lượt là hình chiếu của A và B trên cạnh CD.
Suy ra ABHK là hình chữ nhật và AB =HK = 1
![]()
Quay hình thang ABCD quanh cạnh AB, ta được một khối tròn xoay có thể tích là V = V 1 - 2 V 2 Trong đó:
+ V1 là thể tích của khối trụ có bán kính đáy r =AH =1 chiều cao h =CD =3
Ta có V = V 1 - 2 V 2 (đvtt).
+ V2 là thể tích của khối nón có bán kính đáy r =AH -1; chiều cao h ' = D H = 1
Ta có V 2 = 1 3 πr 2 h ' = 1 3 π đvtt (đvtt).
Vậy thể tích khối tròn xoay cần tính là V = 3 π - 2 . 1 3 π = 7 3 π (đvtt)
Đúng 0
Bình luận (0)
Cho hình thang cân ABCD có đáy nhỏ
A
B
1
, đáy lớn
C
D
3
, cạnh bên
B
C
D
A
2
.
Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng: A.
4
3
π
B.
5
3
π
C.
2...
Đọc tiếp
Cho hình thang cân ABCD có đáy nhỏ A B = 1 , đáy lớn C D = 3 , cạnh bên B C = D A = 2 . Cho hình thang đó quay quanh AB thì được vật tròn xoay có thể tích bằng:
A. 4 3 π
B. 5 3 π
C. 2 3 π
D. 7 3 π
Đáp án D
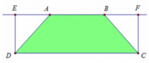
Ta có A E = B F = 1 Khi đó D E = A D 2 − A E 2 = 1
Khi quay hình chữ nhật DEFC quay trục AB ta được hình trụ có thể tích là: V 1 = π . D E 2 . D C = π 1 2 .3 = 3 π
Khi quay tam giác AED quanh trục AB ta được hình nón
có thể tích là V 2 = 1 3 π . D E 2 . A E = 1 3 π .1 2 .1 = π 3 . Do đó thể tích vật tròn xoay tạo thành khi cho hình thang đó quay quanh AB là: V = V 1 − 2 V 2 = 7 π 3 .
Đúng 0
Bình luận (0)
cho hình thang ABCD co đáy AB dài =3\5 đáy lớn CD; nối A với C; nối B với D thì cắt tại O diện tích hình OCD là 15 cm2. Tính diện tích hình thang ABCD
Cho hình thang ABCD có \(\widehat{A}=\widehat{D}=90^o\) và 2 đường chéo vuông góc với nhau tại O.
a) C/m hình thang có chiều cao bằng trung bình nhân 2 đáy
b) Cho AB= 9, CD= 16. Tính diện tích ABCD
c) Tính OA, OB, OC, OD
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân. A. D ( 4;3;0 ) B. D
164
49
;
51
49
;
48
49
C. D
1...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hình thang cân ABCD có AB là đáy lớn, CD là đáy nhỏ và A ( 3;-1;-2 ); B ( 1;5;1 ); C ( 2;3;3 ). Tìm tọa độ điểm D của hình thang cân.
A. D ( 4;3;0 )
B. D 164 49 ; 51 49 ; 48 49
C. D 1 2 ; 1 3 ; 1 4
D. D ( -4;3;0 )
Vì ABCD là hình thang cân nên AD = BC = 3.
Gọi ∆ là đường thẳng qua C và song song với AB.
Gọi (S) là mặt cầu tâm A bán kính R = 3. Điểm D cần tìm là giao điểm của ∆ và (S).
Đường thẳng ∆ có vectơ chỉ phương A B → - 2 ; 6 ; 3 nên có phương trình:
x = 2 - 2 t y = 3 + 6 t z = 3 + 3 t
Phương trình mặt cầu
S : x - 3 2 + y + 1 2 + z + 2 2 = 9 .
Tọa độ điểm D là nghiệm của phương trình
- 2 t - 1 2 + 6 t + 4 2 + 3 t + 5 2 = 9 ⇔ 49 t 2 + 82 t + 33 = 0 ⇔ t = - 1 t = - 33 49 .
Đáp án B
Đúng 0
Bình luận (0)








