Cho tam giác A,B,C. Gọi D,E lần lượt là các \(\overrightarrow{BD}=\frac{2}{3}\overrightarrow{BC}\); \(\overrightarrow{AE}=\frac{1}{4}\overrightarrow{Ac}\). Điểm K trên đoạn thẳng AD sao cho 3 điểm B,K,E thẳng hàng. Tìm tỉ số AD/AK

Những câu hỏi liên quan
Cho tam giác ABC. Gọi D, E lần lượt là các \(\overrightarrow{BD}=\frac{1}{3}\overrightarrow{BC};\overrightarrow{AE}=\frac{3}{4}\overrightarrow{AC}\). Tìm vị trí của điểm K trên AD sao cho 3 điểm B, K, E thẳng hàng.
Bài này có 1 cách cực kì nhanh, ko cần phân tích vecto, đó là sử dụng Menelaus của lớp 8:
Nếu B, K, E thẳng hàng, xét tam giác ACD có BE lần lượt cắt 3 cạnh tam giác tại E, K, B nên theo Menelaus ta có:
\(\frac{EA}{EC}.\frac{BC}{BD}.\frac{DK}{KA}=1\Leftrightarrow\frac{3}{1}.\frac{3}{1}.\frac{DK}{KA}=1\Rightarrow AK=9DK\Rightarrow AK=\frac{9}{10}AD\)
Vậy điểm K nằm ở vị trí sao cho \(\overrightarrow{AK}=\frac{9}{10}\overrightarrow{AD}\) thì B, K, E thẳng hàng
Đúng 0
Bình luận (1)
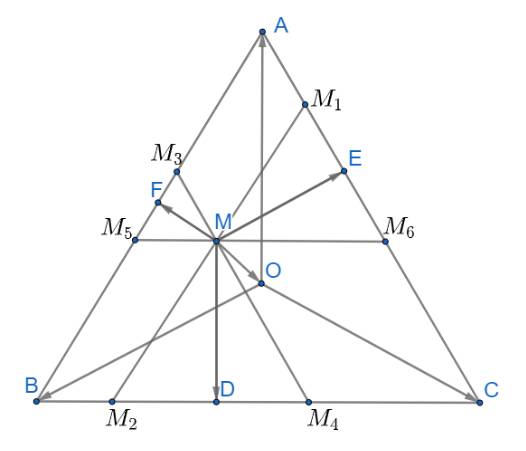
Cho tam giác đều ABC có O là trọng tâm và M là một điểm tùy ý trong tam giác. Gọi D, E, F lần lượt là chân đường vuông góc hạ từ M đến BC, AC, AB. Chứng minh rằng \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \left( {\overrightarrow {MO} + \overrightarrow {OD} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OE} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OF} } \right)\)
Qua M kẻ các đường thẳng \({M_1}{M_2}//AB;{M_3}{M_4}//AC;{M_5}{M_6}//BC\)
Từ đó ta có: \(\widehat {M{M_1}{M_6}} = \widehat {M{M_6}{M_1}} = \widehat {M{M_4}{M_2}} = \widehat {M{M_2}{M_4}} = \widehat {M{M_3}{M_5}} = \widehat {M{M_5}{M_3}} = 60^\circ \)
Suy ra các tam giác \(\Delta M{M_3}{M_5},\Delta M{M_1}{M_6},\Delta M{M_2}{M_4}\) đều
Áp dụng tính chất trung tuyến \(\overrightarrow {AM} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\)(với M là trung điểm của BC) ta có:
\(\overrightarrow {ME} = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right);\overrightarrow {MD} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right);\overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( \Rightarrow \overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
Ta có: các tứ giác \(A{M_3}M{M_1};C{M_4}M{M_6};B{M_2}M{M_5}\) là hình bình hành
Áp dụng quy tắc hình bình hành ta có
\(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_4}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_6}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_3}} + \overrightarrow {M{M_5}} } \right)\)
\( = \frac{1}{2}\left( {\overrightarrow {M{M_1}} + \overrightarrow {M{M_3}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_2}} + \overrightarrow {M{M_5}} } \right) + \frac{1}{2}\left( {\overrightarrow {M{M_4}} + \overrightarrow {M{M_6}} } \right)\)
\( = \frac{1}{2}\overrightarrow {MA} + \frac{1}{2}\overrightarrow {MB} + \frac{1}{2}\overrightarrow {MC} = \frac{1}{2}\left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)\)
\( = \frac{1}{2}\left( {\left( {\overrightarrow {MO} + \overrightarrow {OA} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OB} } \right) + \left( {\overrightarrow {MO} + \overrightarrow {OC} } \right)} \right)\)
\( = \frac{1}{2}\left( {3\overrightarrow {MO} + \left( {\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} } \right)} \right) = \frac{3}{2}\overrightarrow {MO} \) (đpcm)
Vậy \(\overrightarrow {MD} + \overrightarrow {ME} + \overrightarrow {MF} = \frac{3}{2}\overrightarrow {MO} \)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD. Chứng minh rằng:
a) \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
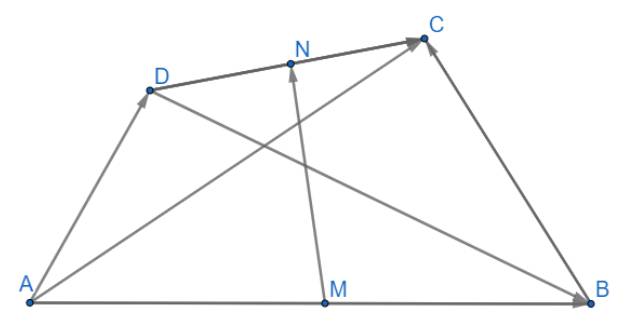
a) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {ND} \\= \left( {\overrightarrow {AM} + \overrightarrow {BM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) \\= \overrightarrow 0 + 2\overrightarrow {MN} + \overrightarrow 0 = 2\overrightarrow {MN} \) (đpcm)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
\(\)\(\overrightarrow {BC} + \overrightarrow {AD} = \overrightarrow {BM} + \overrightarrow {MN} + \overrightarrow {NC} + \overrightarrow {AM} + \overrightarrow {MN} + \overrightarrow {ND} \)
\(\left( {\overrightarrow {BM} + \overrightarrow {AM} } \right) + \left( {\overrightarrow {MN} + \overrightarrow {MN} } \right) + \left( {\overrightarrow {NC} + \overrightarrow {ND} } \right) = 2\overrightarrow {MN} \)
Mặt khác ta có: \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
Suy ra \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
Cách 2:
\(\begin{array}{l}
\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \\
\Leftrightarrow \overrightarrow {AC} - \overrightarrow {AD} = \overrightarrow {BC} - \overrightarrow {BD} \\
\Leftrightarrow \overrightarrow {DC} = \overrightarrow {DC} (đpcm)
\end{array}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC , gọi M, N lần lượt là trung điểm AB, AC . Trên đường thẳng MN, BC lần lượt lấy điểm E, F sao cho \(\overrightarrow{ME}=-\frac{1}{2}\overrightarrow{NE},\overrightarrow{BF}=\frac{1}{3}\overrightarrow{BC}\) chứng minh 3 đểm A,E,F thẳng hàng
Cho tứ giác ABCD. Gọi M, N, P lần lượt là trung điểm của AD, BC và AC. Biết MP PN . Chọn câu đúng.A.overrightarrow{AC} overrightarrow{BD} B.overrightarrow{AC} overrightarrow{BC} C. overrightarrow{AD} overrightarrow{BC} D. overrightarrow{AD} overrightarrow{BD}
Đọc tiếp
Cho tứ giác ABCD. Gọi M, N, P lần lượt là trung điểm của AD, BC và AC. Biết MP PN . Chọn câu đúng.
A.\(\overrightarrow{AC}\) = \(\overrightarrow{BD}\)
B.\(\overrightarrow{AC}\) = \(\overrightarrow{BC}\)
C. \(\overrightarrow{AD}\)= \(\overrightarrow{BC}\)
D. \(\overrightarrow{AD}\)= \(\overrightarrow{BD}\)
Cho tam giác đều ABC, tâm O. M là một điểm bất kì trong tam giác. Hình chiếu vuông góc của M xuống 3 cạnh của tam giác là D, E, F. Từ M kẻ ba đường thẳng song song với 3 cạnh của tam giác. Các giao điểm với các cạnh lần lượt là: I, J, K, L, P, Q (D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ). Chứng minh:overrightarrow{MD}frac{overrightarrow{MI}+overrightarrow{MQ}}{2};overrightarrow{ME}frac{overrightarrow{MK}+overrightarrow{MP}}{2};overrightarrow{MF}frac{overrigh...
Đọc tiếp
Cho tam giác đều ABC, tâm O. M là một điểm bất kì trong tam giác. Hình chiếu vuông góc của M xuống 3 cạnh của tam giác là D, E, F. Từ M kẻ ba đường thẳng song song với 3 cạnh của tam giác. Các giao điểm với các cạnh lần lượt là: I, J, K, L, P, Q (D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ). Chứng minh:
\(\overrightarrow{MD}=\frac{\overrightarrow{MI}+\overrightarrow{MQ}}{2}\);\(\overrightarrow{ME}=\frac{\overrightarrow{MK}+\overrightarrow{MP}}{2}\);\(\overrightarrow{MF}=\frac{\overrightarrow{MJ}+\overrightarrow{ML}}{2}\)
Bạn xem lại đề ạ!
Nếu bạn đã chứng minh được D là trung điểm IQ; E là trung điểm KP; E là trung điểm KP; F là trung điểm LJ
Thì dễ dàng suy ra được: \(\overrightarrow{MD}=\frac{\overrightarrow{MI}+\overrightarrow{MQ}}{2}\); \(\overrightarrow{ME}=\frac{\overrightarrow{MK}+\overrightarrow{MP}}{2}\); \(\overrightarrow{MF}=\frac{\overrightarrow{MJ}+\overrightarrow{ML}}{2}\)
( Vì chúng ta có tính chất: Nếu I là trung điểm đoạn thẳng AB thì mọi điểm M ta có: \(2\overrightarrow{MI}=\overrightarrow{MA}+\overrightarrow{MB}\))
cho tứ giác ABCD . gọi M,N lần lượt là trung điểm AB và CD .cmr: a) 2overrightarrow{mn}overrightarrow{AC}+overrightarrow{BD}overrightarrow{BC}+overrightarrow{AD}b)Lấy H trên AD , K trên BC sao cho dfrac{HA}{HD}dfrac{KB}{KC}. HK cắt MN tại I .cmr I là trung điểm HK
Đọc tiếp
cho tứ giác ABCD . gọi M,N lần lượt là trung điểm AB và CD .cmr:
a) 2\(\overrightarrow{mn}\)=\(\overrightarrow{AC}\)+\(\overrightarrow{BD}\)=\(\overrightarrow{BC}\)+\(\overrightarrow{AD}\)
b)Lấy H trên AD , K trên BC sao cho \(\dfrac{HA}{HD}\)=\(\dfrac{KB}{KC}\). HK cắt MN tại I .cmr I là trung điểm HK
Cho tam giác $A B C$ có trọng tâm $G$. Cho các điểm $D, E, F$ lần lượt là trung điểm của $B C, C A$ $A B$ và $I$ là giao điểm của $A D$ và $E F$. Đạ̄t $\vec{u}=\overrightarrow{A E}, \vec{v}=\overrightarrow{A F}$. Hāy phân tích các vectơ $\overrightarrow{A I}, \overrightarrow{A G}, \overrightarrow{D E}$, $\overrightarrow{D C}$ theo hai vectơ $\vec{u}, \vec{v}$.
Xem thêm câu trả lời
Cho ΔABC có E, I lần lượt là trung điểm của BC và AB. Gọi D, J, K là các điểm thõa mãn \(\overrightarrow{BE}=2\overrightarrow{BD}\), \(\overrightarrow{AJ}=\frac{1}{2}\overrightarrow{JC}\), \(\overrightarrow{IK}=m\overrightarrow{IJ}\).
Tìm m để A, K, D thẳng hàng.





















