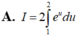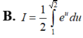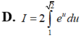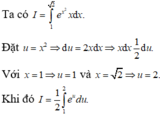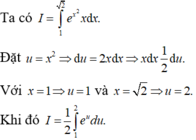Sử dụng công thức biến đổi tích thành tổng và đặt \(a + b = u;\,\,a - b = v\) biến đổi các biểu thức sau thành tích: \(\cos u + \cos v;\,\,\cos u - \cos v;\,\,\sin u + \sin v;\,\,\sin u - \sin v\)
Những câu hỏi liên quan
Trong các công thức biến đổi tích thành tổng ở Mục 3, đặt \(u = a - b,\;v = a + b\) và viết các công thức nhận được.
Ta có: \(u = a - b;v = a + b\).
Suy ra \(u + v = 2a \to a = \frac{{u + v}}{2}\)
\(u - v = 2b \to b = \frac{{u - v}}{2}\)
Ta có: \(\cos u + \cos v = 2\cos \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\)
\(\cos u - \cos v = - 2\sin \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\)
\(\sin u + \sin v = 2\sin \frac{{u + v}}{2}\cos \frac{{u - v}}{2}\)
\(\sin u - \sin v = 2\cos \frac{{u + v}}{2}\sin \frac{{u - v}}{2}\)
Đúng 0
Bình luận (0)
Hãy nhắc lại:
a) Các hằng đẳng thức lượng giác cơ bản;
b) Công thức cộng;
c) Công thức nhân đôi;
d) Công thức biến đổi tích thành tổng và tổng thành tích.
a) Các hằng đẳng thức lượng giác cơ bản:
sin2α + cos2α = 1
1 + tan2α = 1/(cos2α); α ≠ π/2 + kπ, k ∈ Z
1 + cot2α = 1/(sin2α); α ≠ kπ, k ∈ Z
tanα.cotα = 1; α ≠ kπ/2, k ∈ Z
b) Công thức cộng:
cos(a - b) = cosa cosb + sina sinb
cos(a + b) = cosa cosb - sina sinb
sin(a - b) = sina cosb - cosa sinb
sin(a + b) = sina.cosb + cosa.sinb
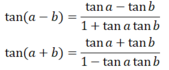
c) Công thức nhân đôi:
sin2α = 2 sinα cosα
cos2α = cos2α - sin2α = 2cos2α - 1 = 1 - 2sin2α
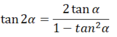
d) Công thức biến đổi tích thành tổng:
cos a cosb = 1/2 [cos(a - b) + cos(a + b) ]
sina sinb = 1/2 [cos(a - b) - cos(a + b) ]
sina cosb = 1/2 [sin(a - b) + sin(a + b) ]
Công thức biến đổi tổng thành tích:
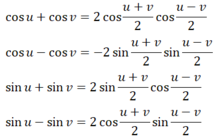
Đúng 0
Bình luận (0)
12 tháng 9 2016 lúc 16:07
sử dụng công thức biến đổi tích thành tổng hay tổng thành tích để giải các phương trình sau :
a) \(\cos x\cos5x=\cos2x\cos4x\)
b) \(\cos5x\sin4x=\cos3x\sin2x\)
c) \(\sin2x+\sin4x=\sin6x\)
d) \(\sin x+\sin2x=\cos x+\cos2x\)
13 tháng 9 2016 lúc 18:22
sử dụng công thức biến đổi tích thành tổng hay tổng thành tích để giải các phương trình sau :
a) \(\cos x\cos5x=\cos2x\cos4x\)
b) \(\cos5x\sin4x=\cos3x\sin2x\)
c) \(\sin2x+\sin4x=\sin6x\)
d) \(\sin x+\sin2x=\cos x+\cos2x\)
16 tháng 9 2016 lúc 20:42
sử dụng công thức biến đổi tích thành tổng hay tổng thành tích để giải các phương trình sau :
a) \(\cos x\cos5x=\cos2x\cos4x\)
b) \(\cos5x\cos4x=\cos3x\cos2x\)
c) \(\sin2x+\sin4x=\sin6x\)
d) \(\sin x+\sin2x=\cos x+\cos2x\)
13 tháng 9 2016 lúc 18:22
sử dụng công thức biến đổi tích thành tổng hay tổng thành tích để giải các phương trình sau :
a) \(\cos x\cos5x=\cos2x\cos4x\)
b) \(\cos5x\sin4x=\cos3x\sin2x\)
c) \(\sin2x+\sin4x=\sin6x\)
d) \(\sin x+\sin2x=\cos x+\cos2x\)
trang 20 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 17:01
Áp dụng công thức biến đổi tích thành tổng cho hai góc lượng giác \(\alpha = \frac{{\alpha + \beta }}{2},\beta = \frac{{\alpha - \beta }}{2}\) ta được đẳng thức nào?
Ta có:
\(\begin{array}{l}\cos \alpha \cos \beta = \cos \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \alpha + \cos \beta } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \sin \beta = \sin \frac{{\alpha + \beta }}{2}\sin \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\cos \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right) - \cos \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\cos \beta - \cos \alpha } \right)\end{array}\)
\(\begin{array}{l}\sin \alpha \cos \beta = \sin \frac{{\alpha + \beta }}{2}\cos \frac{{\alpha - \beta }}{2}\\ = \frac{1}{2}\left[ {\sin \left( {\frac{{\alpha + \beta }}{2} + \frac{{\alpha - \beta }}{2}} \right) + \sin \left( {\frac{{\alpha + \beta }}{2} - \frac{{\alpha - \beta }}{2}} \right)} \right]\\ = \frac{1}{2}\left( {\sin \alpha + \sin \beta } \right)\end{array}\)
Đúng 0
Bình luận (0)
Xét tích phân
I
∫
1
2
x
.
e
x
2
. Sử dụng phương pháp đổi biến số với
u
x
2
, tích phân I được biến đổi thành dạng nào sau đây: A.
I
2
∫
1
2...
Đọc tiếp
Xét tích phân I = ∫ 1 2 x . e x 2 . Sử dụng phương pháp đổi biến số với u = x 2 , tích phân I được biến đổi thành dạng nào sau đây:
A. I = 2 ∫ 1 2 e u d u
B. I = 1 2 ∫ 1 2 e u d u
C. I = 1 2 ∫ 1 2 e u d u
D. 2 ∫ 1 2 e u d u
Xét tích phân
I
∫
1
2
x
e
x
2
d
x
. Sử dụng phương pháp đổi biến số với
u
x
2
, tích phân I được biến đổi thành dạng nào sau đây:
Đọc tiếp
Xét tích phân I = ∫ 1 2 x e x 2 d x . Sử dụng phương pháp đổi biến số với u = x 2 , tích phân I được biến đổi thành dạng nào sau đây:
