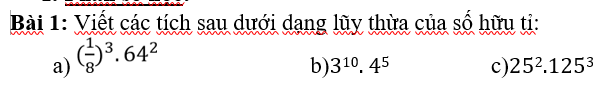\(u_8=u_5.q^{8-5}\Rightarrow-16=2.q^3\Rightarrow q=-2\)

\(u_5=u_1.q^4\Rightarrow u_1=\dfrac{u_5}{q^4}=\dfrac{2}{\left(-2\right)^4}=\dfrac{1}{8}\)

\(u_{21}=u_1.q^{20}=\dfrac{1}{8}.\left(-2\right)^{20}=2^{17}\)

\(\left\{{}\begin{matrix}u_2+u_5-u_4=10\left(1\right)\\u_3+u_6-u_5=20\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u_2+u_5-u_4=10\\u_2.q+u_5.q-u_4.q=20\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u_2+u_5-u_4=10\\q.\left(u_2+u_5-u_4\right)=20\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}u_2+u_5-u_4=10\\q.10=20\end{matrix}\right.\)

\(\Rightarrow q=2\)

\(\left(1\right)\Rightarrow u_1.q+u_1.q^4-u_1.q^3=10\)

\(\Leftrightarrow u_1.\left(q+q^4-q^3\right)=10\)

\(\Leftrightarrow u_1.=\dfrac{10}{\left(q+q^4-q^3\right)}=\dfrac{10}{2+2^4-2^3}=1\)

Vậy \(u_1=1;q=2\)

a: Xét ΔADC có OE//DC
nên \(\dfrac{OE}{DC}=\dfrac{AO}{AC}\left(1\right)\)

Xét ΔBDC có OF//DC

nên \(\dfrac{OF}{DC}=\dfrac{BO}{BD}\left(2\right)\)

Xét ΔOAB và ΔOCD có

\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)

\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)

Do đó: ΔOAB~ΔOCD

=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)

=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)

=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)

=>\(\dfrac{AC}{AO}=\dfrac{BD}{BO}\)

=>\(\dfrac{AO}{AC}=\dfrac{BO}{BD}\left(3\right)\)

Từ (1),(2),(3) suy ra OE=OF
b: Xét ΔCAB có OF//AB

nên \(\dfrac{OF}{AB}=\dfrac{CO}{CA}\)

\(\dfrac{OE}{DC}+\dfrac{OF}{AB}=\dfrac{AO}{AC}+\dfrac{CO}{CA}=\dfrac{AC}{AC}=1\)

=>\(\dfrac{OE}{AB}+\dfrac{OE}{CD}=1\)

=>\(OE\left(\dfrac{1}{AB}+\dfrac{1}{CD}\right)=1\)

=>\(\dfrac{1}{AB}+\dfrac{1}{CD}=\dfrac{1}{OE}\)

Ngày thứ 2 bán được : \(2.\dfrac{2}{9}=\dfrac{4}{9}\left(mảnh.vải\right)\)

Sau 2 ngày bán còn lại : \(1-\left(\dfrac{2}{9}+\dfrac{4}{9}\right)=\dfrac{1}{3}\left(mảnh.vải\right)\)

Đáp số...

P là trung điểm của AB

=>\(\left\{{}\begin{matrix}x_A+x_B=2\cdot x_P=2\cdot\left(-1\right)=-2\\y_A+y_B=2\cdot3=6\end{matrix}\right.\)(3)

N là trung điểm của AC

=>\(\left\{{}\begin{matrix}x_A+x_C=2\cdot x_N=2\cdot2=4\\y_A+y_C=2\cdot y_N=2\cdot2=4\end{matrix}\right.\)(2)

M là trung điểm của BC

=>\(\left\{{}\begin{matrix}x_B+x_C=2\cdot x_M=2\cdot2=4\\y_B+y_C=2\cdot y_M=2\cdot0=0\end{matrix}\right.\)(1)

Từ (1),(2),(3) ta có hệ phương trình:

\(\left\{{}\begin{matrix}x_A+x_B=-2\\x_A+x_C=4\\x_B+x_C=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_A+x_B-x_A-x_C=-2-4=-6\\x_A+x_C=4\\x_B+x_C=4\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x_B-x_C=-6\\x_B+x_C=4\\x_A+x_C=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_B-x_C+x_B+x_C=-6+4=-2\\x_B+x_C=4\\x_A+x_C=4\end{matrix}\right.\)

=>\(\begin{matrix}2x_B=-2\\\end{matrix}\)

=>\(x_B=-1\)

Từ (1),(2),(3) ta có hệ phương trình:

\(\left\{{}\begin{matrix}y_A+y_B=6\\y_A+y_C=4\\y_B+y_C=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y_B-y_C=6-4=2\\y_B+y_C=0\\y_A+y_B=6\end{matrix}\right.\)

=>\(y_B-y_C+y_B+y_C=2+0=2\)

=>\(2\cdot y_B=2\)

=>\(y_B=1\)

Vậy: B(-1;1)

\(\overrightarrow{IA}=\left(2;0\right);\overrightarrow{IB}=\left(-2;3\right);\overrightarrow{IC}=\left(x_C-1;y_C+1\right)\)

Ta có : \(\overrightarrow{IA}+\overrightarrow{IB}+\overrightarrow{IC}=\overrightarrow{0}\) (\(I\) là trọng tâm \(\Delta ABC\))

\(\Leftrightarrow\overrightarrow{IC}=-\overrightarrow{IA}-\overrightarrow{IB}\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_C-1=-2+2\\y_C+1=0-3\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_C=1\\y_C=-4\end{matrix}\right.\) \(\Rightarrow C\left(1;-4\right)\)

\(\overrightarrow{AB}=\overrightarrow{DC}\left(hbh\right)\)

\(\Leftrightarrow\left(-4;3\right)=\left(1-x_D;-4-y_D\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_D=5\\y_D=-7\end{matrix}\right.\) \(\Rightarrow D\left(5;-7\right)\)

\(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{0}\) (O là trung điểm AC)

\(\Leftrightarrow\left(3-x_O;-1-y_O\right)=-\left(1-x_O;-4-y_O\right)\)

\(\Leftrightarrow\left\{{}\begin{matrix}3-x_O=x_O-1\\-1-y_O=y_O+4\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_O=2\\y_O=-\dfrac{5}{2}\end{matrix}\right.\) \(\Rightarrow O\left(2;-\dfrac{5}{2}\right)\)

\(P\in Oy\Leftrightarrow P\left(0;y_D\right)\)

\(G\in Ox\Leftrightarrow G\left(x_G;0\right)\)

\(G\) là trọng tâm \(\Delta MNP\)

\(\Rightarrow y_G=\dfrac{y_M+y_N+y_P}{3}\)

\(\Leftrightarrow y_P=3y_G-y_M-y_N=3.0+1+3=4\)

Vậy \(P\left(0;4\right)\)

b, \(3^{10}.4^5=\left(3^2\right)^5.4^5=9^5.4^5=\left(9.4\right)^5=36^5\)
\(c,25^2.125^3=\left(5^2\right)^2.\left(5^3\right)^3=5^4.5^9=5^{4+9}=5^{13}\)

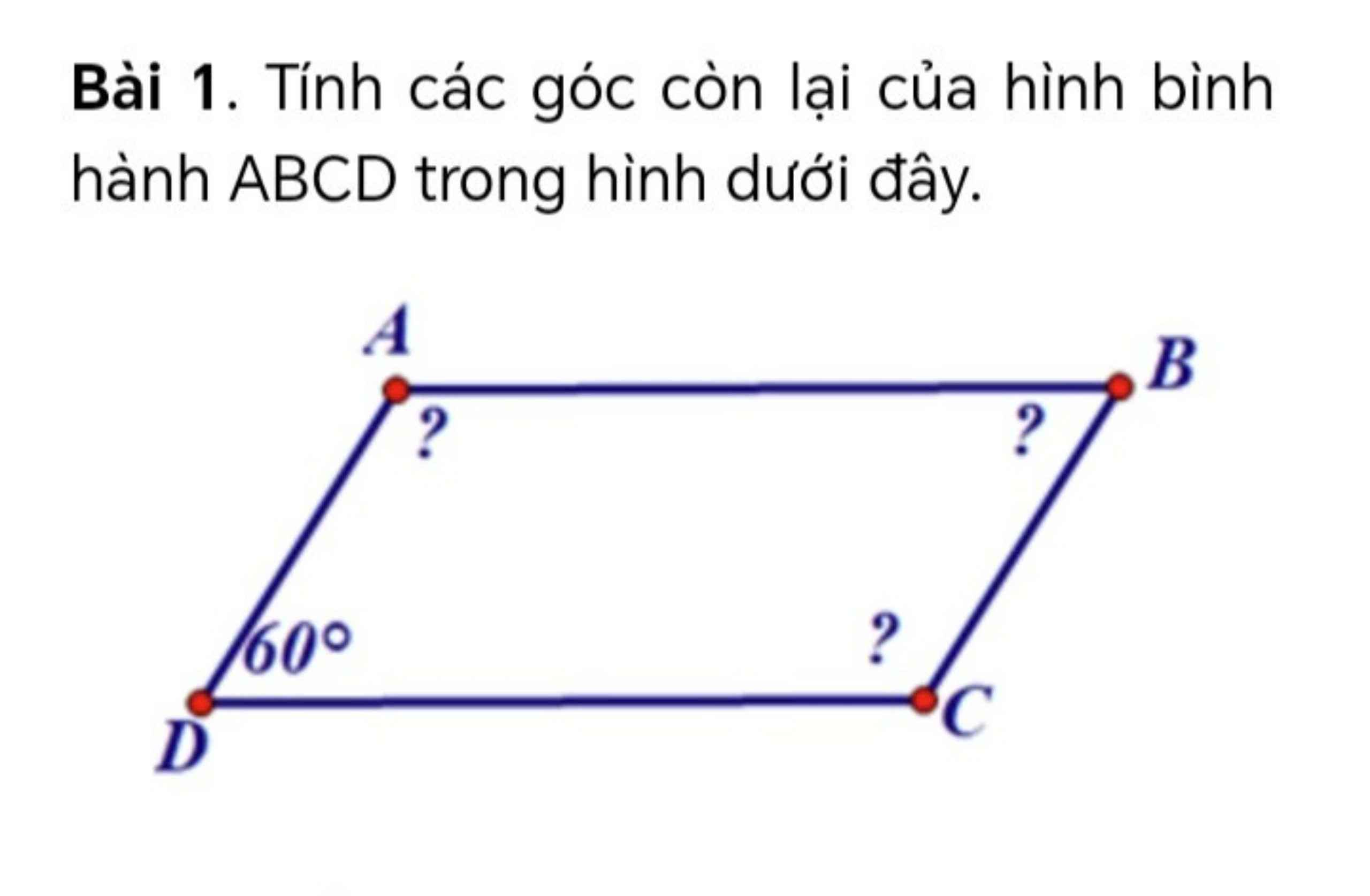
Ta có:D=B(theo định lí hình bình hành)

Do đó:B=60 độ

Mà A=C

Nên A=C=360-60+60

                 _________=120 độ

                        3

Vậy D=B=60 độ

A=C=120 độ