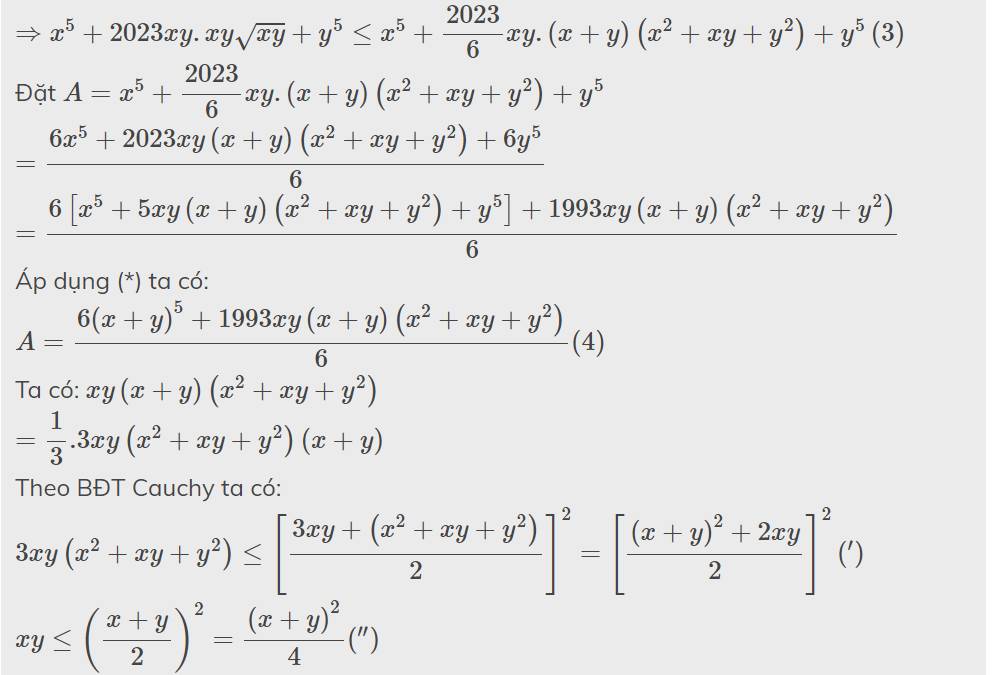CÔNG BỐ ĐÁP ÁN CÂU ĐỐ QUY LUẬT 1,2,4,8,16,31,?Đáp án chính xác: 57, 99, 163.Quy luật dãy số: thứ tự các số trong dãy số là n tượng trưng cho số hình nhỏ được chia bởi việc lấy 1 hình tròn có n điểm (không thẳng hàng) và nối chéo tất cả các điểm với nhau. Công thức tính số hình đó là: A1+C^n_2+C^n_4. Với n 7, 8 và 9 ta sẽ thu được các kết quả trên.Tuy nhiên, vẫn có một số đáp án khác được chấp nhận, mặc dù có thể giải thích chưa thuyết phục:Những bạn Lương Quý và Nguyễn Lê Huy Hoàng sẽ nhận 6GP...
Đọc tiếp
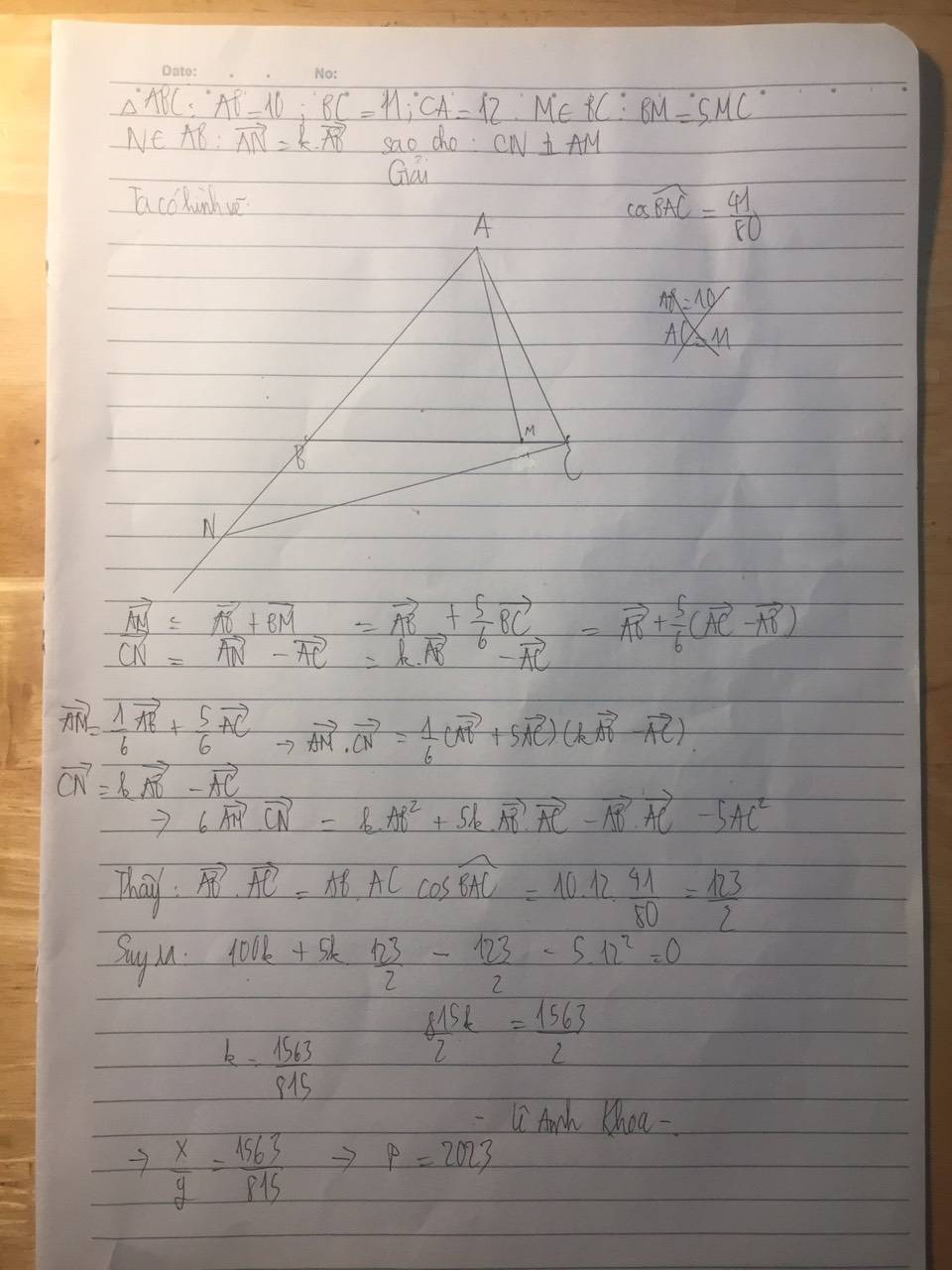
CÔNG BỐ ĐÁP ÁN CÂU ĐỐ QUY LUẬT 1,2,4,8,16,31,?
Đáp án chính xác: 57, 99, 163.
Quy luật dãy số: thứ tự các số trong dãy số là n tượng trưng cho số hình nhỏ được chia bởi việc lấy 1 hình tròn có n điểm (không thẳng hàng) và nối chéo tất cả các điểm với nhau. Công thức tính số hình đó là: \(A=1+C^n_2+C^n_4\). Với n = 7, 8 và 9 ta sẽ thu được các kết quả trên.
Tuy nhiên, vẫn có một số đáp án khác được chấp nhận, mặc dù có thể giải thích chưa thuyết phục:

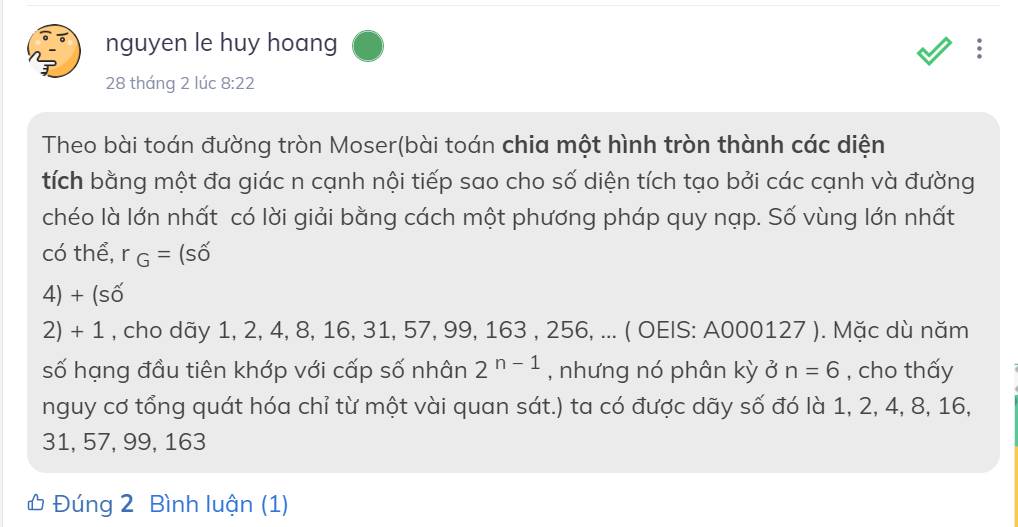
Những bạn Lương Quý và Nguyễn Lê Huy Hoàng sẽ nhận 6GP vì đã đưa ra câu trả lời khá đúng nhé!
Ngoài ra, sự kiện IELTS Speaking Mock Test - Season 1 chỉ còn mở đơn đăng kí vé Miễn phí còn 2 ngày thôi đó. Với vé VIP, chúng mình sẽ mở 9 ngày nữa! Link: https://forms.gle/LbbWiQiDsxQFQWTJ9
![]()
![]() Các em đừng quên có hẹn với Thi đấu OLM vào tối nay, thứ sáu, ngày 24/03/2023 nhé!
Các em đừng quên có hẹn với Thi đấu OLM vào tối nay, thứ sáu, ngày 24/03/2023 nhé!