[Câu hỏi Xuân Quý Mão 2023 - môn Toán]
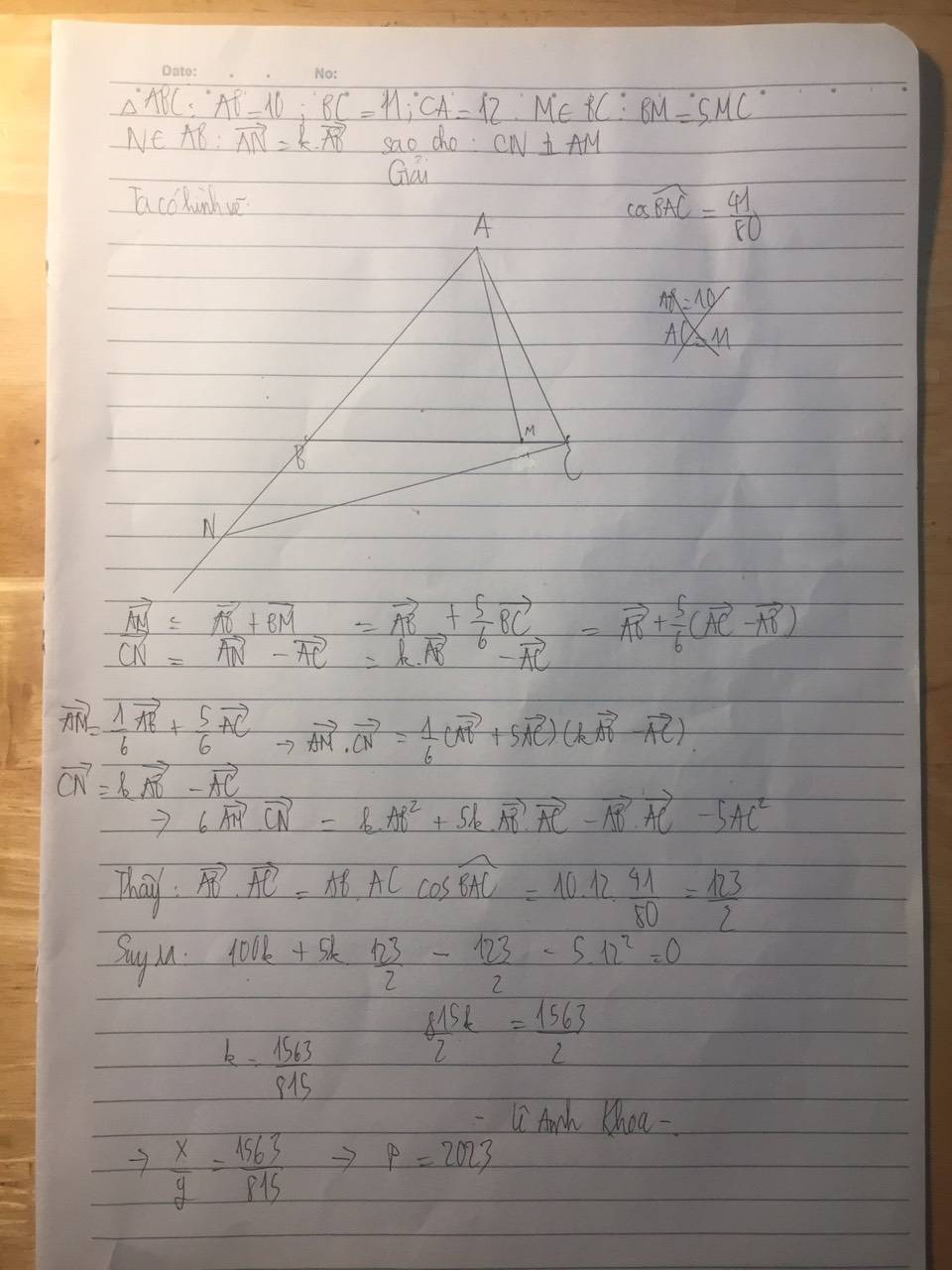
Cho tam giác ABC có \(AB=10;BC=11;CA=12.\) Gọi M thuộc cạnh BC thỏa mãn BM = 5MC và N thuộc đường thẳng AB sao cho \(\overrightarrow{AN}\) \(=k\overrightarrow{AB}\), với \(k\in R\). Biết \(k=\dfrac{x}{y}\) (\(x,y\in Z\), phân số tối giản) sao cho \(CN\perp AM\). Tính giá trị biểu thức: \(P=\sqrt{2022x-2023y+2580888}\).
không biết đúng không, góp thử bài làm heheh
Từ tam giác ABC có AB = 10 ; BC = 11 ; CA = 12
=> \(cosC=\dfrac{AC^2+BC^2-AB^2}{2AC.BC}=\dfrac{11^2+12^2-10^2}{2.11.12}=\dfrac{5}{8}\)
tương tự cosB = \(\dfrac{7}{20}\)
cos A = \(\dfrac{41}{80}\)
Lại có \(CN\perp AM\)
nên \(\overrightarrow{CN}.\overrightarrow{AM}=0\)
\(\Leftrightarrow(\overrightarrow{CA}+\overrightarrow{AN}).(\overrightarrow{AC}+\overrightarrow{CM})=0\)
\(\Leftrightarrow(\overrightarrow{CA}+k\overrightarrow{AB})(\overrightarrow{AC}+\dfrac{1}{5}\overrightarrow{CB})=0\)
\(\Leftrightarrow-AC^2+\dfrac{1}{5}CA.CB.cosC+kAB.AC.cosA+\dfrac{1}{5}k.AB.BC.cos(180^{\text{o}}-B)=0\)
\(\Leftrightarrow-12^2+\dfrac{1}{5}.12.11.\dfrac{5}{8}+k.10.12.\dfrac{41}{80}+\dfrac{1}{5}k.10.11.(-\dfrac{7}{20})=0\)
\(\Leftrightarrow k=\dfrac{1275}{538}=\dfrac{x}{y}\) tối giản => (x ; y) = (1275;538) ; (-1275,-538) (x;y \(\inℤ\))
Với (x,y) = (1275,538)
=> P = \(\sqrt{2022.1275-2023.538+2580888}=\sqrt{4070564}\)
Với (x;y) = (-1275 ; -538)
=> P = \(\sqrt{1091212}\)
Mình sửa lại chỗ
\((\overrightarrow{CA}+k\overrightarrow{AB)}(\overrightarrow{AC}+\dfrac{1}{6}\overrightarrow{CB})=0\)
\(\Leftrightarrow-AC^2+\dfrac{1}{6}.CA.CB.cosC+k.AB.AC.cosA+\dfrac{1}{6}.k.AB.CB.cos\left(180^{\text{o}}-B\right)=0\)
\(\Leftrightarrow-12^2+\dfrac{1}{6}.12.11.\dfrac{5}{8}+k.10.12.\dfrac{41}{80}+\dfrac{1}{6}k.10.11.\dfrac{-7}{20}=0\)
\(\Leftrightarrow k=\dfrac{1563}{661}=\dfrac{x}{y}\)
Vì x;y nguyên ; phân số tối giản nên
(x;y) = (1563;661) ; (-1563;-661)
Với (x,y) = (1563;661)
=> P = \(\sqrt{2022.1563-2023.661+2580888}=\sqrt{4404071}\)
Với (x;y) = (-1563;-661)
=> P = \(\sqrt{-2022.1563+2023.661+2580888}=\sqrt{757705}\)
eheheheh tối qua bánh chưng, bánh tét quá =))) ghi với vẽ hình sai tè le =))) nay đã sửa lại rồi heheh
