cho tam giác cân abc có ab bằng ac Trên tia đối của BC lấy D trên tia đối của CB lấy E sao cho BD = BC = C Chứng minh rằng góc BAD bằng góc CAE nhỏ hơn góc BAC

Những câu hỏi liên quan
cho tam giác cân abc có ab bằng ac Trên tia đối của BC lấy D trên tia đối của CB lấy E sao cho BD = BC = C Chứng minh rằng góc BAD bằng góc CAE nhỏ hơn góc BAC
Giúp mk nha
cho tam giác ABC cân tại A. Trên tia đối BC lấy D. Trên tia đối CB lấy E sao cho DB=BC=CE. Chứng minh góc BAD = góc CAE nhỏ hơn góc BAC
Cho tam giác ABC cân tại A.Trên cạnh BC lấy điểm D và E ( D nằm giữa B và E) sao cho BD=DE=EC
a) Chứng minh góc BAD bằng góc CAE
b) Chứng minh AD < AC
c) Trên tia đối của tia EA lấy điểm K sao cho EK = EA.Chứng minh góc BAD = CAE và nhỏ hơn góc DAE
Tam giác ABC cân tại A => AB = AC
=> Góc ABD = góc ACE
Xét tam giác ABD và tam giác ACE
AB = AC ( cmt )
Góc ABD = góc ACE ( cmt )
BD = CE ( gt )
=> Tam giác ABD = tam giác ACE ( c.g.c )
=> Góc BAD = góc CAE ( 2 góc tương ứng )
=> AD = AC ( 2 cạnh tương ứng )
Xét tam giác ADE và tam giác ACE
AD = AC ( cmt )
DE = EC( gt )
AE chung
=> tam giác ADE= tam giác ACE ( c.c.c )
=> góc DAE = góc EAC ( 2 góc tương ứng )
Ta có: góc BAD = góc EAC ( cmt )
Góc DAE = góc EAC ( cmt )
=> góc BAD = góc DAE = góc EAC
a) Ta có: tam giác ABC cân tại A (gt)
=> Góc B = góc C1, AB = AC (định lí)
Xét tam giác ABD và tam giác ACE có:
AB = AC (chứng minh trên)
BD = CE (gt)
Góc B = góc C1 (chứng minh trên)
=> Tam giác ABD = tam giác ACE (c.g.c)
=> Góc BAD = góc CAE (2 góc tương ứng) (đpcm)
b) Ta có: tam giác ABD = tam giác ACE (chứng minh trên)
=> AB = AC (2 cạnh tương ứng)
Xét tam giác ADE và tam giác CEK có:
DE = CE (gt)
Góc AED = góc CEK (2 góc đối đỉnh)
AE = EK (gt)
=> Tam giác ADE = tam giác CKE (c.g.c)
=> AD = CK (2 cạnh tương ứng)
Kẻ đường cao AH
Ta có: DH < AH
=> AD < AB mà AB = AC (chứng minh trên)
=> AC > AD (đpcm)
c) Ta có: AD < AC
Mà AD = CK (2 cạnh tương ứng)
=> CK < AC
Xét tam giác ACK có AC > CK
=> Góc CAK < góc K (định lí)
Lại có: góc BAD = góc CAE (chứng minh trên)
=> Góc BAD < góc K
Mà góc K = DAE (vì tam giác ADE = tam giác KCE)
=> Góc BAD < góc DAE
hay góc BAD = góc CAE < góc DAE (đpcm)
Cho tam giác ABC có AB =AC và AB>BC. Trên tia đối của tia BC lấy D, trên tia đối của tia CB lấy E sao cho DB= BC =CE.
Chứng minh: Góc BAD= góc CAE < góc BAC
Cho tam giác ABC cân tại A. Trên tia đối BC lấy điểm D, Trên tia đối của tia CB lấy điểm E sao cho ∠BAD = ∠CAE. Kẻ BH vuông góc với AD (H ∈ AD). kẻ CK vuông góc với AE (K ∈ AE). Chứng minh rằng : BD = CE
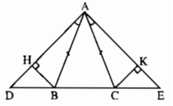
+) Do tam giác ABC cân tại A nên ∠ABC = ∠ACB (1)
Lại có; ∠ABC + ∠ABD = 180º ( hai góc kề bù) (2)
∠ACB + ∠ACE = 180º ( hai góc kề bù) (3)
Từ (1); (2); (3) suy ra: ∠ABD = ∠ACE
+) Xét ΔABD và ΔACE có:
∠DAB = ∠EAC ( giả thiết)
AB = AC (vì tam giác ABC cân tại A)
∠ABD = ∠ACE ( chứng minh trên )
⇒ ΔABD = ΔACE (g.c.g)
⇒ BD = CE ( hai cạnh tương ứng)..
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho góc BAD= góc CAE. Kẻ BH vuông góc với AD, kẻ CK vuông góc với AE. Chứng minh:
a) BD=CE
b) BH=CK
a) Do ΔABC cân tại A
=> AB = AC; góc ABC=góc ACB
Lại có: góc ABC+ góc ABD = 180o (kề bù)
góc ACB + góc ACE = 180o (kề bù)
=> góc ABD = góc ACE
Xét ΔADB và ΔAEC có:
góc BAD = góc CAE (gt)
AB = AC (cmt)
góc ABD = góc ACE (cmt)
=> ΔADB = ΔAEC (g.c.g)
=> BD = CE (2 cạnh tg ứng) đpcm
b) Vì ΔADB = ΔAEC (câu a)
=> góc ADB = góc AEC (2 góc t/ư)
hay góc HDB = góc KEC
Xét ΔBHD vuông tại H và ΔCKE vuông tại E có:
BD = CE (câu a)
góc HDB = góc KEC(cmt)
=> ΔBHD = ΔCKE (ch - gn)
=> BH = CK (2 cạnh tg ứng) (đpcm)
Đúng 3
Bình luận (0)
Cho tam giác ABC cân tại A (có ABAC góc A tù) trên cạnh BC lấy điểm D trên tia đối của CB lấy E sao cho BD CE trên tia đối của tia CA lấy điểm I sao cho CI C câu 1 a) chứng minh rằng tam giác ABC bằng tam giác ABC b) AB + AC AB + AE câu 2 từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt AB;AI theo thứ tự tại M; N Chứng minh BM CN câu 3 Chứng minh rằng chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN
Đọc tiếp
Cho tam giác ABC cân tại A (có AB=AC góc A tù) trên cạnh BC lấy điểm D trên tia đối của CB lấy E sao cho BD = CE trên tia đối của tia CA lấy điểm I sao cho CI = C
câu 1 a) chứng minh rằng tam giác ABC bằng tam giác ABC
b) AB + AC< AB + AE
câu 2 từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt AB;AI theo thứ tự tại M; N Chứng minh BM = CN
câu 3 Chứng minh rằng chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN
đây e ơi https://olm.vn/hoi-dap/question/541217.html
Đúng 0
Bình luận (1)
Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Thị Ngọc Ánh - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC cân (AB=AC, góc A tù). Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Trên tia đối của tia CA lấy điểm I sao cho CI=CA
a) Chứng minh: Tam giác ABD bằng tam giác ICE.
b) Từ D và E kẻ các đường thẳng cùng vuông góc với BC cắt AB, AI theo thứ tự tại M,N. Chứng minh: BM=CN.
c) Chứng minh rằng chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN.
Xem thêm câu trả lời
cho tam giác abc vuông tại a AB lớn Hơn AC AB=8 BC=10 gọi M là trung điểm của BC Trên tia đối của MA lấy D sao cho MD=MA vẽ AH vuông góc với BC tại H trên tia đối của HA lấy E sao cho HE=HA chứng minh rằng a, CD vuông góc vơi AC , tam giác CAE cân C, BD=CE d, AE vông góc với ED
a/ Xét 2 tam giác MDC và MAB có MA=MD (gt), MB=MC (gt), góc DMC=góc AMB (đối đỉnh)
=> tam giác MDC = tam giác MAB
=> Góc CBA=góc BCD (Góc tương ứng)
Xét \(\Delta ABC\)có \(\widehat{CBA}+\widehat{ACB}=90^0\)(Tính chất Tam giác vuông)
=> \(\widehat{BCD}+\widehat{ACB}=90^0=\widehat{ACD}\) => \(CD\perp AC\)
b/ Xét 2 tam giác vuông CHE và CHA có: CH (chung); HE=HA (gt); Tam giác vuông tại H
=> \(\Delta CHE=\Delta CHA\)=> CA=CE (2 cạnh tương ứng) => \(\Delta CAE\)cân tại C
Đúng 0
Bình luận (0)




















