3. Cho tam giác ABC vuông tại A, có BD là tia phân giác. Kẻ DH vuông góc với BC (E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh :a) BD là đường trung trực AEb) DFDCc) ADDC4. Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt AC tại E. Kẻ EH vuông góc với BC( H thuộc BC). GỌi K là giao điểm của AB và HE. Chứng minh rằng: a) tam giác ABE tam giác HBEb) BE là đường trung trực của đoạn thẳng AH.c) EK EC và AE EC5. Cho tam giác ABC cân tại A (AB AC), trung tuyến AM. Gọi D là mộ...
Đọc tiếp
3. Cho tam giác ABC vuông tại A, có BD là tia phân giác. Kẻ DH vuông góc với BC (E thuộc BC). Gọi F là giao điểm của BA và ED. Chứng minh :
a) BD là đường trung trực AE
b) DF=DC
c) AD<DC
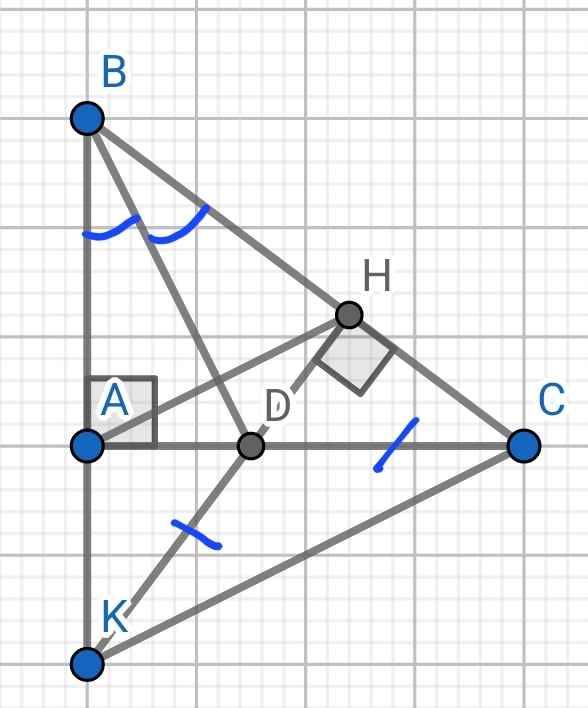
4. Cho tam giác ABC vuông tại A, tia phân giác của góc ABC cắt AC tại E. Kẻ EH vuông góc với BC( H thuộc BC). GỌi K là giao điểm của AB và HE. Chứng minh rằng:
a) tam giác ABE = tam giác HBE
b) BE là đường trung trực của đoạn thẳng AH.
c) EK = EC và AE < EC
5. Cho tam giác ABC cân tại A (AB = AC), trung tuyến AM. Gọi D là một điểm nằm giữa A và M.
Chứng minh :
a) AM là tia phân giác góc A
b) tam giác ABD = tam giác ACD
c) tam giác BCD là tam giác cân
6. Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Từ D kẻ DH vuông góc với BC tại H và DH cắt AB tại K.
a) Chứng minh : AD=DH
b) So sánh độ dài hai cạnh AD và DC
c) Chứng minh tam giác KBC là tam giác cân