Tim x
(a-5)(a+1) > 0
(a+1)(4-a) < 0
(a3+1)(a3+30) < 0
Nếu a 3 / 3 > a 2 / 2 và log b ( 3 / 4 ) < log b ( 4 / 5 ) thì:
A. 0 < a < 1, b > 1 B. 0 < a < 1, 0 < b < 1
C. a > 1, b > 1 D. a > 1, 0 < b < 1
Nếu a 3 / 3 > a 2 / 2 và log b 3 / 4 < log b 4 / 5 thì:
A. 0 < a < 1, b > 1 B. 0 < a < 1, 0 < b < 1
C. a > 1, b > 1 D. a > 1, 0 < b < 1
Câu 35: Cách nhập hàm nào sau đây không đúng?
A. =SUM(A1, 0) B. =SUM(0; A3) C. =Sum(5, a3) D. =Sum(5, 0)
Câu 36: Xác định đâu là hàm đúng khi tính giá trị trung bình các dãy số?
A. =SUM(5, A3) B. =AVERAGE(0; A3) C. =Sum(5, 0.1) D. =Average(0, 1)
Câu 37: Công thức = 5^2*3 cho kết quả bao nhiêu?
A. 30 B. 40 C. 55 D. 75
Câu 38: Để tính hiệu giá trị trong các ô E3 và F7, sau đó nhân với 10% ta thực hiện bằng công thức nào sau đây?
A. E3 - F7 * 10%. B. (E3 - F7) * 10%
C. = (E3 - F7) * 10% D. =E3 - (F7 * 10%)
Câu 39: Trong chương trình bảng tính, công thức nào sau đây là đúng:
A. = (18+5)*3 + 23 B. = (18+5).3 + 2^3
C. = (18+5)*3 + 2^3 D. = (18+5).3 + 23
Bài 1:
a) Cho a + b + c = 0. CMR: a3 + b3+ c3 = 3abc
b) Cho a3 + b3 + c3 = 3abc và a. b, c đôi một khác nhau. CMR: a + b + c = 0
a: Ta có: \(a+b+c=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)
Ta có: a+b+c=0
\(\Leftrightarrow\left(a+b+c\right)^3=0\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(a+c\right)\left(b+c\right)=0\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow a^3+b^3+c^3=3abc\)
b: Ta có: \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
\(\Leftrightarrow a+b+c=0\)
a) \(a^3+b^3+c^3=3abc\Leftrightarrow\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc=0\Leftrightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)(đúng do a+b+c = 0)
b) Ta có: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\\\left(b-c\right)^2\ge0\\\left(c-a\right)^2\ge0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a^2+b^2\ge2ab\\b^2+c^2\ge2bc\\c^2+a^2\ge2ac\end{matrix}\right.\Rightarrow a^2+b^2+c^2\ge ab+ac+bc\)
\(ĐTXR\Leftrightarrow a=b=c\), mà a,b,c đôi một khác nhau => Đẳng thức không xảy ra\(\Rightarrow a^2+b^2+c^2>ab+ac+bc\Rightarrow a^2+b^2+c^2-ab-ac-bc>0\)
Ta có: \(a^3+b^3+c^3=3abc\Leftrightarrow\left(a+b\right)^3+c^3-3a^2b-3ab^2-3abc=0\Leftrightarrow\left(a+b+c\right)\left[\left(a+b\right)^2-\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2-3ab\right)=0\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)\(\Rightarrow a+b+c=0\)( do (1))
Bài 1:
a) Cho a + b + c = 0. CMR: a3 + b3+ c3 = 3abc
b) Cho a3 + b3 + c3 = 3abc và a. b, c đôi một khác nhau. CMR: a + b + c = 0
a: Ta có: a+b+c=0
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\a+c=-b\\b+c=-a\end{matrix}\right.\)
Ta có: a+b+c=0
\(\Leftrightarrow\left(a+b+c\right)^3=0\)
\(\Leftrightarrow a^3+b^3+c^3+3\left(a+b\right)\left(b+c\right)\left(a+c\right)=0\)
\(\Leftrightarrow a^3+b^3+c^3-3abc=0\)
\(\Leftrightarrow a^3+b^3+c^3=3abc\)
b: Ta có: \(a^3+b^3+c^3=3abc\)
\(\Leftrightarrow\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+2ab+b^2-ac-bc+c^2\right)-3ab\left(a+b+c\right)=0\)
\(\Leftrightarrow\left(a+b+c\right)\left(a^2+b^2+c^2-ab-ac-bc\right)=0\)
\(\Leftrightarrow a+b+c=0\)
Cho hệ phương trình ( a + b ) x + ( a - b ) y = 2 ( 1 ) ( a 3 + b 3 ) x + a 3 - b 3 y = 2 ( a 2 + b 2 ) ( 2 )
Với a ≠ ± b , a b ≠ 0 hệ có nghiệm duy nhất bằng:
![]()
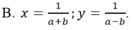
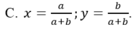
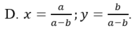
Rút gọn biểu thức P = a 3 - 1 3 + 1 a 4 - 5 . a 5 - 2 (với a > 0 v à a ≠ 1 )
A. P = 1
B. P = a
C. P = 2
D. P = a 2
Xét a,b là các số thực thỏa mãn:
1. a3 + a = 3 và b3 + b = 3. Chứng minh rằng a=b.
2. a3+ 3a2+ 4a - 2 =0 và b3- 3b2 + 4b - 7 =0. Tính a + b ?
10:591. b3+b= 3
(b3+b)=3
b.(3+1)=3
b. 4= 3
b=\(\dfrac{3}{4}\)
a3+a= 3 b3
(a3+a)=3
a.(3+1)=3
a. 4= 3
a=\(\dfrac{3}{4}\)
2
Cho n số a1, a2, a3, ... , an mà mỗi số bằng 1 hoặc -1. Gọi Sn= a1.a2+a2.a3+a3.a4+...+an-1.an+an.a1
a) Chứng tỏ: S5 khác o
b) Chứng tỏ S6 khác 0
c) Chứng tỏ rằng: Sn=0 khi và chỉ khi n chia hết cho 4