
Những câu hỏi liên quan
Đố ai giải được: Tìm tích của tất cả các số tự nhiên?
0 vi trong cac so tu nhien co so 0 nen 0 nhan bao nhieu cung bang 0
Đúng 0
Bình luận (0)
1.Chứng tỏ rằng với mọi số tự nhiên n thì tích (n+4) x (n+7) là một số chẵn.
2.tìm tất cả các số tự nhiên a và b sao cho ab =246 và a<b
Cau 2.
vi a.b= 246 nen suy ra a,b la U(246). Vi a < b nen ta co bang
a 1 2 3 6
b 246 123 82 41
Vay co 4 truong hop xay ra
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số tự nhiên khác 0 sao cho ƯCLN của hai số đó là 8 và tích của hai số đó là 384.
Mọi người giúp mình với
Giải:
VÌ ƯCLN(a;b)= 8 nên ta có: \(\left\{{}\begin{matrix}a=8k\\b=8d\end{matrix}\right.\)
Theo bài ra ta có: 8k.8d = 384
kd = 384 : (8.8)
kd = 6
Vậy kd là ước của 6; 6 = 2,3 ⇒ Ư(6) = {1; 2; 3; 6}
Lập bảng ta có:
| k | 1 | 2 | 3 | 6 |
| a = 8k | 8 | 16 | 24 | 48 |
| d | 6 | 3 | 2 | 1 |
| b = 8d | 48 | 24 | 16 | 8 |
Theo bảng trên ta có:
(a; b) = (8; 48); (16; 24); (24; 16); (48; 8)
Kết luận các cặp số thỏa mãn đề bài là:
(a; b) =(8; 48); (16; 24); (24; 16); (48; 8)
Đúng 0
Bình luận (0)
tìm tất cả các số tự nhiên sao cho tích (a+1).(b-1)=20. Cảm ơn mọi người ạ
20 = 1.20 = 20.1 = 4.5 = 5.4 = 2.10 = 10.2
Ta lập bảng sau:
Đúng 0
Bình luận (0)
Mọi người làm bai ay mình với
Cho hai số tự nhiên a và b. Tìm tất cả các số tự nhiên c sao cho trong ba số, tích của hai số luôn chia hết cho số còn lại.
Tìm tất cả các số tự nhiên n , biết rằng n + S(n) = 2014 với S(n) là tổng các chữ số của n ? help me !!
mọi người giúp mình a ! van xin đó !! _ _"
Bài 2.
a) Tìm tất cả các số tự nhiên n vừa là ước của 70 và là bội của 7.
b) Tìm tất cả các số tự nhiên n vừa là ước của 225 và là bội của 9.
Xem chi tiết
\(a,Ư\left(70\right)=\left\{1;2;5;7;10;14;35;70\right\}\\ B\left(7\right)=\left\{0;7;14;21;28;35;42;49;56;63;72;81;90;99;....\right\}\\ \Rightarrow n\in\left\{7;14;35;70\right\}\\ b,Ư\left(225\right)=\left\{1;3;5;9;15;25;45;75;225\right\}\\ B\left(9\right)=\left\{0;9;18;27;36;45;54;63;72;81;...;216;225;234;243;...\right\}\\ \Rightarrow n\in\left\{9;45;225\right\}\)
Đúng 0
Bình luận (0)
Tìm tất cả các số tự nhiên N biết rằng tổng tất cả các ước số của N bằng 2N và tích tất cả các ước số của N bằng N^2
Mọi người giúp em 4 bài này với mọi người giải bằng tiếng việt hay là tiếng anh cũng dc ạ (tiếng anh thì tốt ạ)bài 1:Gọi n là số tự nhiên sao cho n + 1 và 2n + 1 đều là số chính phương . Chứng minh rằng n chia hết cho 24.bài2:Tìm tất cả các số tự nhiên n sao cho 2n + 1,3n + 1 đều là bình phương hoàn hảo và 6n + 5 là số nguyên tố.bài3:tìm các số nguyên a, b, c sao cho a^4 + b^4 7c^4 +5.bài4:Tìm tất cả các số nguyên dương x, y và các số nguyên tố p sao cho x^2 −3xy + p^2y^2 12p.
Đọc tiếp
Mọi người giúp em 4 bài này với mọi người giải bằng tiếng việt hay là tiếng anh cũng dc ạ (tiếng anh thì tốt ạ)
bài 1:Gọi n là số tự nhiên sao cho n + 1 và 2n + 1 đều là số chính phương . Chứng minh rằng n chia hết cho 24.
bài2:Tìm tất cả các số tự nhiên n sao cho 2n + 1,3n + 1 đều là bình phương hoàn hảo và 6n + 5 là số nguyên tố.
bài3:tìm các số nguyên a, b, c sao cho a^4 + b^4 = 7c^4 +5.
bài4:Tìm tất cả các số nguyên dương x, y và các số nguyên tố p sao cho x^2 −3xy + p^2y^2 = 12p.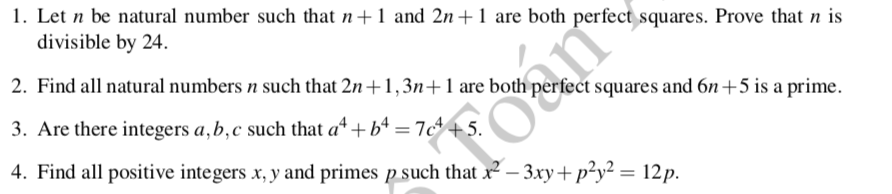
1.
\(2n+1\) luôn lẻ \(\Rightarrow2n+1=\left(2a+1\right)^2=4a^2+4a+1\Rightarrow n=2a\left(a+1\right)\)
\(\Rightarrow n\) chẵn \(\Rightarrow n+1\) lẻ \(\Rightarrow\) là số chính phương lẻ
\(\Rightarrow n+1=\left(2b+1\right)^2=4b^2+4b+1\)
\(\Rightarrow n=4b\left(b+1\right)\)
Mà \(b\left(b+1\right)\) là tích 2 số tự nhiên liên tiếp \(\Rightarrow\) luôn chẵn
\(\Rightarrow4b\left(b+1\right)⋮8\Rightarrow n⋮8\)
Mặt khác số chính phương chia 3 chỉ có các số dư 0 và 1
Mà \(\left(n+1\right)+\left(2n+1\right)=3n+2\) chia 3 dư 2
\(\Rightarrow n+1\) và \(2n+1\) đều chia 3 dư 1
\(\Rightarrow n⋮3\)
\(\Rightarrow n⋮24\) do 3 và 8 nguyên tố cùng nhau
Đúng 2
Bình luận (0)
2.
Lý luận tương tự bài 1, ta được n chẵn
Mặt khác các số chính phương chia 5 chỉ có các số dư 0, 1, 4
Mà: \(\left(2n+1\right)+\left(3n+1\right)=5n+2\) chia 5 dư 2
\(\Rightarrow2n+1\) và \(3n+1\) đều chia 5 dư 1
\(\Rightarrow2n⋮5\Rightarrow n⋮5\) (do 2 và 5 nguyên tố cùng nhau)
\(\Rightarrow n=5k\Rightarrow6n+5=5\left(6k+1\right)\)
- TH1: \(k=0\Rightarrow n=0\Rightarrow6n+5\) là SNT (thỏa mãn)
- TH2: \(k>0\Rightarrow6k+1>0\Rightarrow6n+5\) có 2 ước dương lớn hơn 1 \(\Rightarrow\) không là SNT (loại)
Vậy \(n=0\) là giá trị duy nhất thỏa mãn yêu cầu
Đúng 2
Bình luận (0)
Xem thêm câu trả lời


















