
Những câu hỏi liên quan
tìm a và b để đường thẳng (đ) y= (a-2)x + b có hệ số góc bằng 4 và đi qua điểm M(1:3) ?
tìm a và b để đường thẳng (d) :y=(a-2)x+b có hệ số góc bằng 4 và ik qua điểm M(1,-3)
Bài 2. Cho hàm số y(m−1)x+n có đồ thị là đường thẳng d
a) Tìm m và n để đường thẳng d đi qua hai điểm A(1;2), B(2;5).
b) Tìm m và n biết đường thẳng d có hệ số góc bằng 3, cắt trục hoành tại điểm có hoành độ bằng –2.
c) Tìm m và n biết đường thẳng d trùng với đường thẳng d:y5x-3.
Bài 3. a) Cho hai đường thẳng d:y(m-3)x-3m+3, d, :y(2m+1)x+m+5
Tìm m để hai đường thẳng cắt nhau; song song với nhau; vuông góc với nhau; trùng nhau; cắt nhau tại một điểm nằm trên trục tung.
b) Tìm m để ba đường...
Đọc tiếp
Bài 2. Cho hàm số y=(m−1)x+n có đồ thị là đường thẳng d a) Tìm m và n để đường thẳng d đi qua hai điểm A(1;2), B(2;5). b) Tìm m và n biết đường thẳng d có hệ số góc bằng 3, cắt trục hoành tại điểm có hoành độ bằng –2. c) Tìm m và n biết đường thẳng d trùng với đường thẳng d:y=5x-3. Bài 3. a) Cho hai đường thẳng d:y=(m-3)x-3m+3, d, :y=(2m+1)x+m+5 Tìm m để hai đường thẳng cắt nhau; song song với nhau; vuông góc với nhau; trùng nhau; cắt nhau tại một điểm nằm trên trục tung. b) Tìm m để ba đường thẳng d:y=2x+5,d:y=x+2,d :y=mx−12 đồng quy
2
a)
d đi qua A (1;2), B(2;5)
=> Ta có hệ phương trình: \(\left\{{}\begin{matrix}\left(m-1\right).1+n=2\\\left(m-1\right).2+n=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m+n=3\\2m+n=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=4\\n=-1\end{matrix}\right.\)
b)
d có hệ số góc a = 3 => d: y = 3x + n
=> m -1 = 3 <=> m = 4
d cắt Ox tại x = -2, y = 0 \(\Leftrightarrow0=3.\left(-2\right)+n\) => n = 6
c)
d trùng d' \(\Rightarrow\left\{{}\begin{matrix}m-1=5\\n=-3\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}m=6\\n=-3\end{matrix}\right.\)
Đúng 1
Bình luận (0)
1.Tìm a và b để đường thẳng (d): (a - 2)x + b có hệ số góc bằng 4 và đi qua điểm M(1;-3).
Đường thẳng d có hệ số góc bằng 4 ↔ a - 2 = 4 ↔ a = 6
Mặt khác (d) đi qua điểm M (1;-3) nên thay a = 6, x = 1; y = -3 vào y = (a - 2)x + b.
Khi đó ta có: -3 = (6 - 2).1 + b
→ -3 = 4 + b
→ b = -7
Vậy a = 6 và b = -7 là các giá trị cần tìm và khi đó (d): y = 4x - 7
Đúng 0
Bình luận (0)
d) Tìm a, b để đồ thị hàm số đi qua điểm A(1; 2) và B(2;1)
e) Lập phương trình đường thẳng đi qua gốc toạ độ O và điểm A(1; 2)
f) Lập phương trình đường thẳng (d) đi qua M(2; -1) và vuông góc với đường thẳng (d’) có phương trình: y = −1 2 x +3
Bài 4.
a) Lập phương trình đường thẳng (d) đi qua điểm M (-1; 3) và có hệ số góc bằng 2.
b) Lập phương trình đường thẳng (d) đi qua M(3; 5) và song song với đường thẳng (d’) có phương trình y = 2x
a) Gọi pt đường thẳng (d) là : \(y=ax+b\left(a\ne0\right)\)
Vì (d) có hệ số góc là 2 \(\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(-1;3\right)\)
\(\Rightarrow3=-2+b\Rightarrow b=5\Rightarrow y=2x+5\)
b) Gọi pt đường thẳng d là \(y=ax+b\left(a\ne0\right)\)
Vì \((d)\parallel (d')\Rightarrow a=2\Rightarrow y=2x+b\)
Vì đường thẳng d đi qua điểm \(M\left(3;5\right)\)
\(\Rightarrow5=6+b\Rightarrow b=-1\Rightarrow y=2x-1\)
Đúng 1
Bình luận (2)
1) Cho 2 hàm số y-x+1 và y3x + 2 .a) vẽ đồ thị 2 hàm số trên cùng 1 hệ trục tọa độ .b) Tính góc tạo bởi 2 đường thẳng đó trên trục hoành2) Cho đường thẳng (d) có phương trình y m+1.x-3m+6.Tìm m,n để: .â) (d) // với đường thẳng -2x+5 và đi qua điểm có tọa độ (2 ; -1).b) (d) tạo bởi trục hoành 1 góc tù .c) (d) có hệ số góc bằng -2 và trung độ góc bằng 1.3) Cho hàm số y(m+3).+2m+1 (d1) và y2m.x-3m-4 (d2) â) Tìm m để d1 cắt d2, d1 song song với d2, d1 trùng d2.b) d1 và d2 cắt nhau tại 1 điểm trên...
Đọc tiếp
1) Cho 2 hàm số y=-x+1 và y=3x + 2 .
a) vẽ đồ thị 2 hàm số trên cùng 1 hệ trục tọa độ .
b) Tính góc tạo bởi 2 đường thẳng đó trên trục hoành
2) Cho đường thẳng (d) có phương trình y = m+1.x-3m+6.Tìm m,n để: .
â) (d) // với đường thẳng -2x+5 và đi qua điểm có tọa độ (2 ; -1).
b) (d) tạo bởi trục hoành 1 góc tù .
c) (d) có hệ số góc bằng -2 và trung độ góc bằng 1.
3) Cho hàm số y=(m+3).+2m+1 (d1) và y=2m.x-3m-4 (d2)
â) Tìm m để d1 cắt d2, d1 song song với d2, d1 trùng d2.
b) d1 và d2 cắt nhau tại 1 điểm trên trục trung .
c) d1 và d2 cắt nhau tại 1 điểm trên trục hoành .
đ) Tìm góc tạo bởi 2 đường thẳng với trục Ox khi m =-1
1/ Cho đường thẳng (d): y2x+m+1. Tìm các giá trị của m để đường thẳng (d) cắt trục tung và trục hoành tại A và B sao cho diện tích tam giác OAB bằng 9 (đvdt).2/ Cho parabol (P): yx^2và đường thẳng (d) có hệ số góc là a khác 0 đi qua điểm M(1;2)a/ Cm rằng (d) luôn luôn cắt P tại hai điểm phân biệt với mọi a khác 0.b/ Gọi xA và xB là hoành độ giao điểm của P và d. Chứng minh rằng xA+xB-xA.xB2.3/ Cho đường thẳng d: (m+1)x + (m-3)y1a/ Chứng minh đường thẳng d luôn đi qua một điểm với mọi m và tìm đi...
Đọc tiếp
1/ Cho đường thẳng (d): y=2x+m+1. Tìm các giá trị của m để đường thẳng (d) cắt trục tung và trục hoành tại A và B sao cho diện tích tam giác OAB bằng 9 (đvdt).
2/ Cho parabol (P): y=x^2
và đường thẳng (d) có hệ số góc là a khác 0 đi qua điểm M(1;2)
a/ Cm rằng (d) luôn luôn cắt P tại hai điểm phân biệt với mọi a khác 0.
b/ Gọi xA và xB là hoành độ giao điểm của P và d. Chứng minh rằng xA+xB-xA.xB=2.
3/ Cho đường thẳng d: (m+1)x + (m-3)y=1
a/ Chứng minh đường thẳng d luôn đi qua một điểm với mọi m và tìm điểm cố định đó.
b/ Gọi h là khoảng cách từ O đến đường thẳng d. Tìm các giá trị của m để h lớn nhất.
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k . Tìm k để đường thẳng d cắt đồ thị hàm số C: y x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1? A. k 2 B. k -1 C. k 1 D. Đáp án khác
Đọc tiếp
Gọi d là đường thẳng đi qua điểm A( -1; 0) với hệ số góc k . Tìm k để đường thẳng d cắt đồ thị hàm số C: y= x3-3x2+ 4 tại ba điểm phân biệt A; B; C và tam giác OBC có diện tích bằng 1?
A. k =2
B. k= -1
C. k= 1
D. Đáp án khác
Đường thẳng d đi qua A và có hệ số góc k nên có dạng y= k( x+ 1) hay
Kx- y+k=0 .
Phương trình hoành độ giao điểm của C và d là:
x 3 - 3 x 2 + 4 = k x + k ⇔ ( x + 1 ) ( x 2 - 4 x + 4 - k ) = 0
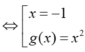
D cắt tại ba điểm phân biệt khi phương trình (*) có hai nghiệm phân biệt khác -1
⇔ ∆ ' > 0 g ( - 1 ) ≠ 0 ⇔ k > 0 k ≠ 9
Khi đó g( x) =0 khi x=2- k ; x = 2 + k Vậy các giao điểm của hai đồ thị lần lượt là
A ( - 1 ; 0 ) ; B ( 2 - k ; 3 k - k k ) ; C ( 2 + k ; 3 k + k k ) .
Tính được
B C = 2 k 1 + k 2 , d ( O , B C ) = d ( O , d ) = k 1 + k 2 .
Khi đó
S ∆ O B C = 1 2 . k k 2 + 1 . 2 k . k 2 + 1 = 1 ⇔ k k = 1 ⇔ k 3 = 1 ⇔ k = 1 .
Vậy k= 1 thỏa yêu cầu bài toán.
Chọn C.
Đúng 0
Bình luận (0)
















