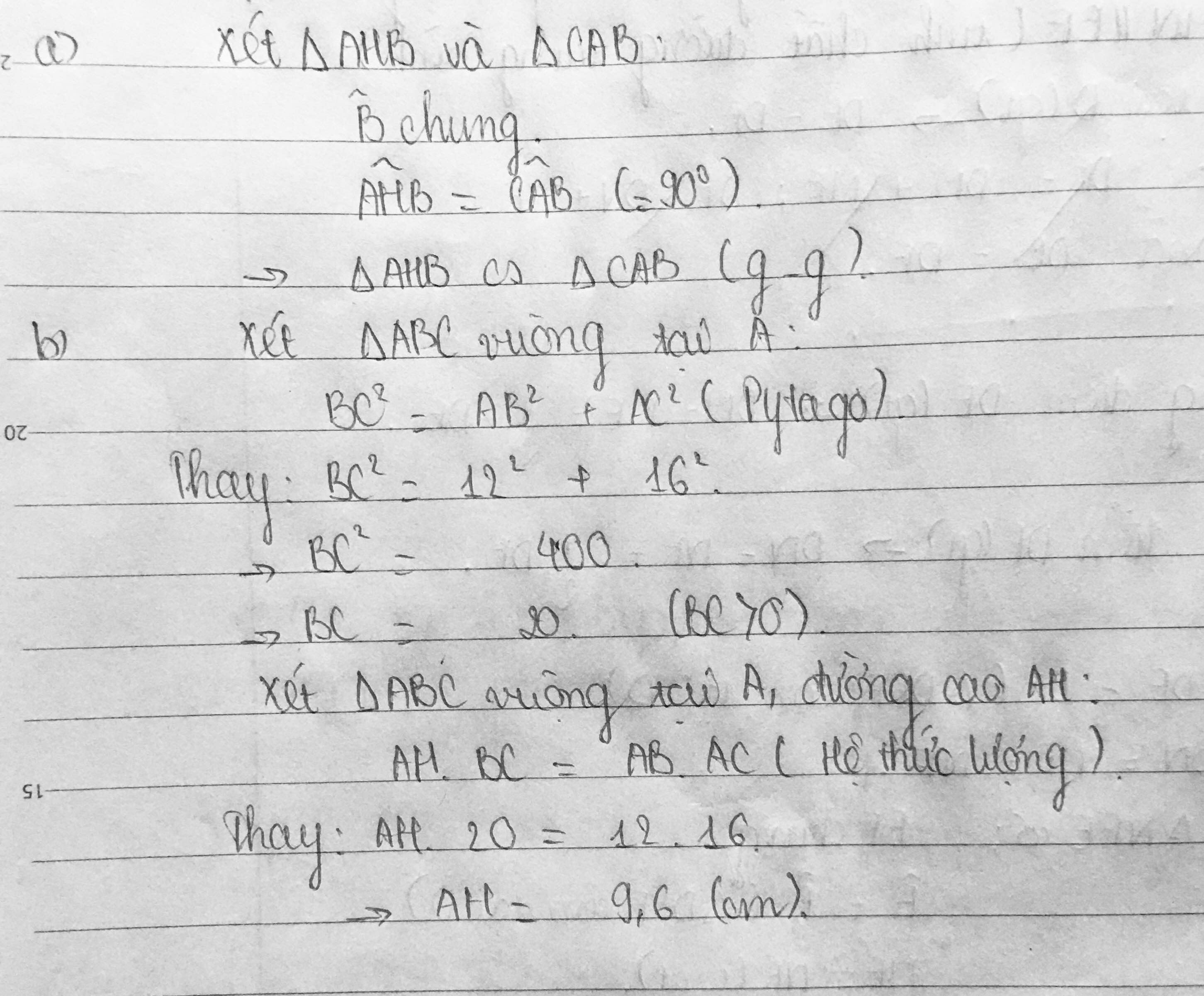Cho tam giác ABC vuông tại A ( AC > AB ) , đường cao AH . a) CM tam giác ABH đồng dạng với tam giác CAB . b) CM AH2 = BH . CH c) Điểm I là trung điểm của AC . Kẻ HK vuông góc với AB ( K thuộc AB ) . D là giao điểm của BI và HK . Chứng minh KD = DH .

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH. a, Chứng minh tam giác AHB đồng dạng với tam giác CAB b, Cho AB=12 cm, AC=16 cm. Tính độ dài AH? c, Kẻ DH vuông góc với AC tại D. Gọi M là trung điểm của AB; CM cắt HD tại I. Chứng minh I là trung điểm của HD
Cho tam giác ABC vuông tại A(AB<AC) đường cao AH, biết BH =9cm,HC =16cm.Gọi M là trung điểm của BC, đường vuông góc với BC tại M cắt AC ở D.
a, CM: tam giác MDC đồng dạng với tam giác ABC
b, CM: AH2=HB.HC
c, Tính MD
d, Gọi k là hình chiếu của M trên AC tính diện tích tam giác KDM
Bạn kham khảo link này nhé.
Câu hỏi của Trần Ngô Anh Tuyền - Toán lớp 8 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
em vô link anh viết ở đó là có
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho tam giác abc vuông tại a , ab<ac , kẻ đường cao ah, phân giác bd. gọi i là giao điểm của ah và bd
a, cm tam giác abd đồng dạng tam giác hbi
b, cm ah2 = hb.hc
c,cm tam giác iad cân va da2 =dc.ih
d, ck vuông góc bd, kd vuông góc ac, q là trung điểm của bc. cm k,p,q thẳng hàng
a: Xét ΔABD vuông tại A và ΔHBI vuông tại H có
\(\widehat{ABD}=\widehat{HBI}\)
Do đó: ΔABD\(\sim\)ΔHBI
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
Đúng 0
Bình luận (0)
A) Ta cần chứng minh tam giác \(ABD\) đồng dạng tam giác \(HBI\). Để làm điều này, ta cần chứng minh rằng các góc của chúng là bằng nhau.
- Góc \(ABD\) và \(HBI\) là góc vuông, vì \(AB\) và \(HB\) là đường cao của tam giác \(ABC\).
- Góc \(ADB\) và \(HIB\) là góc phân giác của tam giác \(ABC\), do đó chúng bằng nhau.
Vậy, ta có thể kết luận tam giác \(ABD\) đồng dạng tam giác \(HBI\).
B) Để chứng minh \(AH^2 = HB \cdot HC\), ta sử dụng định lý đường cao và tính chất của đường cao trong tam giác vuông:
- \(AH\) là đường cao của tam giác \(ABC\), nên \(AH^2 = BH \cdot HC\).
Vậy, \(AH^2 = HB \cdot HC\).
C) Để chứng minh tam giác \(IAD\) cân và \(DA^2 = DC \cdot IH\), ta sử dụng tính chất của giao điểm của đường phân giác và đường cao:
- Góc \(IAD\) và \(IDA\) là góc phân giác của tam giác \(ABC\), do đó chúng bằng nhau.
- \(IH\) là đường cao của tam giác \(ABC\) nên \(DA^2 = DC \cdot IH\).
Vậy, ta chứng minh được tam giác \(IAD\) cân và \(DA^2 = DC \cdot IH\).
D) Để chứng minh \(K, P, Q\) thẳng hàng, ta có thể sử dụng tính chất của điểm trung điểm và đường phân giác:
- \(Q\) là trung điểm của \(BC\), nên \(Q\) nằm trên đường thẳng \(KP\).
- \(K\) là giao điểm của \(AH\) và \(BD\), và \(P\) là giao điểm của \(AH\) và \(CI\), nên \(K, P, Q\) thẳng hàng theo Định lý Menelaus trên tam giác \(ACI\) và đường thẳng \(KQ\).
Vậy, ta đã chứng minh được \(K, P, Q\) thẳng hàng.
Đúng 0
Bình luận (0)
Cho tam giác abc vuông tại a ( ab<ac) có đường cao ah (h thuộc bc)
a) CM tam giác ABC đồng dạng tam giác HBA
b)Tính độ dài bc,bh khi ab=6cm,ac=8cm
c)kẻ hd vuông góc ab tại d. CM ah^2=dh.ac
d) gọi m là trung điểm của ac. kẻ mk vuông góc bc tại k. CM BK^2=AB^2+AC^2
Cho tam giác ABC vuông tại A ( AC > AB ) , đường cao AH .
a) CM tam giác ABH đồng dạng với tam giác CAB .
b) CM AH2 = BH . CH
c) Điểm I là trung điểm của AC . Kẻ HK vuông góc với AB ( K thuộc AB ) . D là giao điểm của BI và HK . Chứng minh KD = DH .
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
DO đo: ΔABH\(\sim\)ΔCBA
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại a đường cao AH h thuộc BC biết AB = 15 cm AC = 20 cm .a)tính độ dài đoạn thẳng bc ah.b) kẻ HM vuông góc với AB HN vuông góc với AC chứng minh tam giác ahb đồng dạng với tam giác ACB .C)gọi I là trung điểm của BC k là giao điểm của AE và MN chứng minh AD vuông góc MN tại k.
Cho tam giác ABC nhọn (AB<AC). các đường cao AE , BF cắt nhau tại H. gọi M là trung điểm của BC qua H vẽ đường thẳng a vuông góc với HM , a cắt AB , Ac lần lượt tại I và K. a) cm: Tam giác ABC ~ Tam giác EFC b) Qua C kẻ đường thẳng b song song với IK , b cắt AH, AB theo thứ tự tại N và D . cm : NC=ND và HI=HK c) Gọi G là giao điểm của CH và AB ,cm: AH/HE + BH/HF + CH/HG > 6
Cho tam giác ABC vuông tại A,đường cao AH.Kẻ HK vuông góc với AC tại K
a)CM:tam giác ABC đồng dạng tam giác HAC;tam giác AHB đồng dạng tam giác HKA
b)CM: AH^2=HK.AB
c)Gọi M là trung điểm của AB,đoạn CM cắt HK tại I.Cm:I là trung điểm của HK
a: Xét ΔABC vuông tại A và ΔHAC vuông tại H có
góc C chung
=>ΔABC đồng dạng với ΔHAC
Xét ΔAHB vuông tại H và ΔHKA vuông tại K có
góc HAB=góc KHA
=>ΔAHB đồng dạng với ΔHKA
b: ΔAHB đồng dạng với ΔHKA
=>AH/HK=AB/HA
=>AH^2=HK*AB
c: Xét ΔCAM có KI//AM
nên KI/AM=CI/CM
Xét ΔCMB có IH//MB
nên IH/MB=CI/CM
=>KI/AM=IH/MB
mà AM=MB
nên KI=IH
=>I là trung điểm của KH
Đúng 0
Bình luận (0)
Bài1: cho tam giác ABC nhọn(AB《AC). Có hai đường cao BE và CF cắt nhau tại H.a) CM: Tam giác ABE đồng dạng với tam giác ACF.b) CM: Tam giác AFE đồng dạng với tam giác ACB.c) Tia phân giác của góc ABE cắt tia phân giác của góc ACF tại K,gọi I,J lần lượt là trung điểm của AH và BC. Cm: I,K,J thẳng hàng.Bài2: Cho tam giác ABC vuông tại A (AB《AC),vẽ đường cao AH. Trên đoạn thẳng HC lấy điểm M (M không trùng với H và C),từ M vẽ MN vuông góc với AC tại N.a) CM:tam giác CMN đồng dạng với tam giác CAH...
Đọc tiếp
Bài1: cho tam giác ABC nhọn(AB《AC). Có hai đường cao BE và CF cắt nhau tại H.
a) CM: Tam giác ABE đồng dạng với tam giác ACF.
b) CM: Tam giác AFE đồng dạng với tam giác ACB.
c) Tia phân giác của góc ABE cắt tia phân giác của góc ACF tại K,gọi I,J lần lượt là trung điểm của AH và BC. Cm: I,K,J thẳng hàng.
Bài2: Cho tam giác ABC vuông tại A (AB《AC),vẽ đường cao AH. Trên đoạn thẳng HC lấy điểm M (M không trùng với H và C),từ M vẽ MN vuông góc với AC tại N.
a) CM:tam giác CMN đồng dạng với tam giác CAH và CA×CN=CH×CM
b) CM: tam giác ACM đồng dạng với tam giác HNC.
c) Trên tia đối của tia AC lấy điểm D sao cho AD《AC. Vẽ AE vuông góc với BD tại E. CM:góc BEH=góc BCN. Gọi K,F lần lượt là trung điểm BH và BD. I là giao điểm của EK và CF. CM: KC×IE=EF×IC.
Bài 1:
a) Xét tam giác ABE và tam giác ACF có:
Góc AEB=góc AFC(=90 độ)
Góc A chung
=>Tam giác ABE đồng dạng vs tam giác ACF (g-g)
b)
Vì tam giác ABE đồng dạng vs tam giác ACF(cmt)
=>\(\frac{AB}{AC}=\frac{AE}{AF}\)
Xét tam giác AFE và tam giác ACB có:
Góc A chung(gt)
\(\frac{AB}{AC}=\frac{AE}{AF}\)
=>Tam giác AFE và tam giác ACB đồng dạng (c-g-c)
c)
H ở đou ra vại? :))