Cho tập XX có 2021 phần tử phân biệt, số các hoán vị của tập XX là
A.
4042
B.
2021!
22021
D.
20212
Cho số hữu tỉ \(x=\frac{a-20}{2021}\)gọi S là tập hợp các số nguyên dương a để x là số hữu tỉ âm.
a) Tính số phần tử của tập S
b) Có bao nhiêu tập con của tập S có hai phần tử
Để x < 0
=> a - 20 < 0
=> a < 20 (1)
mà a \(\inℕ^∗\)(2)
Từ (1) và (2) => \(a\in\left\{1;2;3;...;19\right\}\)
=> Số phần tử của tập S là : (19 - 1) : 1 + 1 = 19 phần tử
b) Số tập con của S có 2 phần tử là :
19 x (19 - 1) : 2 = 171 tập hợp con
a)để x là số hữu tỉ âm thì số nguyên dương a phải lớn hơn 0 và nhỏ hơn 20
xét các trường hợp ta thấy : S=(1;2;3;4;5;6;7;8;9;10;11;12;13;14;15;16;17;18;19)
vậy: S có 19 phần tử
b)vì S có 19 phần tử nên số tập hợp con của S là:
19 x 19 = 361
vậy S số tập hợp con của S có 2 phần tử = 361
(bài này làm đại)
1,Cho tập X có n phần tử trong đó có 2 phần tử a và b.Tính số các hoán vị của tập X sao cho a và b không đứng cạnh nhau?
2,Cho tập X=\(\left\{1;2;3;.....2n\right\}\).Hỏi có bao nhiêu hoán vị của tập X mà các phần tử chẵn sẽ đứng ở vị trí chẵn?
3,Có tất cả bao nhiêu số tự nhiên chẵn gồm 5 chữ số khác nhau được thành lập từ các chữ số 1;2;3;4;5?
4,Gọi A là tập hợp tất cả các số tự nhiên có 7 chữ số đôi một khác nhau được tạo ra từ các chữ số 0;1;2;3;4;5;6.Hỏi có bao nhiêu số thuộc A mà trong số đó có chữ số 1 và cho số 2 đứng cạnh nhau ?
5,Từ 5 học sinh không có bạn nào trùng nhau trong đó có bạn Hoa và Hồng.Hỏi có bao nhiêu cách sắp xếp 5 bạn đó vào 1 bàn dài 5 chỗ sao cho:
a,Số cách xếp là tùy ý.
b,Hoa và Hồng ngồi cạnh nhau.
c,Hoa và Hồng không ngồi cạnh nhau.
d,Hoa và Hồng ngồi cạnh nhau 1 đứa bạn.
e,Hoa và Hồng ở hai đầu bàn.
Cho tập hợp A = x ∈ N | 1980 ≤ x ≤ 2021 . Số phần tử của tập hợp (A) là:
A. 40
B 41
C. 42
D. 43
Đáp án cần chọn là: C
Các số tự nhiên liên tiếp hơn kém nhau 1 đơn vị. Vì vậy số phần tử của tập hợp A là:
2021–1980+1=42.
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x .2 x = x x − m + 1 + m 2 x − 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x .2 x = x x − m + 1 + m 2 x − 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. 2
C. 3
D. Vô số
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x . 2 x = x x - m + 1 + m 2 x - 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. 2
C. 3
D. Vô số
Đáp án B.
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x - m 2 x = x 2 - ( m - 1 ) x - m
⇔ x - m 2 x = ( x - m ) ( x + 1 ) ⇔ x - m 2 x - x - 1 = 0 ⇔ x = m 2 x = x + 1
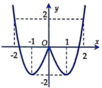
Giải phương trình 2 x = x + 1 .
![]()
Nhìn vào màn hình ta thấy phương trình 2 x = x + 1 có hai nghiệm phân biệt là x = 0 ; x = 1 . Do vậy để tập nghiệm của phương trình đã cho có đúng hai phần tử thì m ∈ 0 ; 1 . Vậy có 2 giá trị của m thỏa mãn, ta chọn B.
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x . 2 x = x x - m + 1 + m 2 x - 1 có hai phần tử.Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Đáp án D
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x . 2 x = x 2 - m x + x + m . 2 x - m
⇔ 2 x x - m = x + 1 x - m ⇔ 2 x - x - 1 x - m = 0 ⇔ [ 2 x - x - 1 = 0 ( 1 ) x - m = 0 ( 2 )
Giải (1) , đặt f x = 2 x - x - 1 . Xét hàm số f x = 2 x - x - 1 trên ℝ , có f ' x = 2 x . ln 2 - 1
Phương trình f ' x = 0 ⇔ 2 x = 1 ln 2 ⇔ x = log 2 1 ln 2 = - log 2 ln 2
⇒ f x = 0 có nhiều nhất 2 nghiệm mà f 0 = f 1 ⇒ f x = 0 ⇔ [ x = 0 x = 1
Để phương trình đã cho có hai nghiệm phân biệt ⇔ 2 có 1 nghiệm hoặc 0
Vậy m = {0;1} là hai giá trị cần tìm.
cho A là một tập hợp có 10 chữ số, A = {0;1;2;..;9}. B là một tập hợp con của A gồm 5 phân tử. CMR: trong tập hợp các số có dạng x+y, với x,y là hai phần tử phân biệt thuộc B, có ít nhất 2 số có cùng chữ số hàng đơn vị
Cho tập hợp A có 3 phần tử, số hoán vị các phần tử của A bằng
A. 5
B. 4
C. 6
D. 7
Chọn C
Số các hoán vị gồm 3 phần tử của A là P 3 = 3! = 6