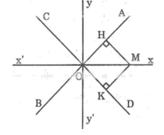
* Xét điểm M nằm trong góc AOD

Kẻ MH ⊥ OA, MK ⊥ OD

Xét hai tam giác MHO và MKO:

∠(MHO) = ∠(MKO) = 90o

MH = MK

OM cạnh huyền chung

Suy ra: ΔMHO = ΔMKO

(cạnh huyền - cạnh góc vuông)

Suy ra: ∠(MOH) = ∠(MOK)(2 góc tương ứng)

Hay OM là tia phân giác của ∠(AOD).

* Ngược lại, M nằm trên tia phân giác của ∠(AOD)

Xét hai tam giác vuông MHO và MKO, ta có:

∠(MHO) = ∠(MKO)= 90o

∠(MOH) = ∠(MOK)

OM cạnh huyền chung

Suy ra: ΔMHO = ΔMKO (cạnh huyền - góc nhọn)

Suy ra: MH = MK (2 cạnh tương ứng)

Vậy tập hợp các điểm M cách đều OA và OD là tia phân giác Ox của góc AOD.

Tương tự M nằm trong các góc AOC, DOB, BOC thì tập hợp các điểm M là tia phân giác Oy, Oy’, Ox’.

Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.

Nếu điểm M nằm trong góc AOD thì kẻ MH vuông góc với OA, MK vuông góc với OD

Xét ΔMHO vuông tại H và ΔMKO vuông tại K có 

MO chung

MH=MK

Do đó: ΔMHO=ΔMKO

Suy ra: \(\widehat{MOH}=\widehat{MOK}\)

=>M nằm trên tia phân giác của góc AOD

Vì ΔMHO=ΔMKO nên MH=MK

=>Tập hợp điểm M cách đều OA và OD là phân giác Ox của góc AOD

Tương tự M nằm trong các góc AOC, DOB, BOC thì tập hợp các điểm M là tia phân giác Oy, Oy’, Ox’.

Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.

Cũng ở Thanh Hóa à bạn😗

ta có △ AEB nội tiếp (T) có AB là đường kính -> AE vuông EB hay AE vuông ME 

xét tứ giác OAEM có góc MOA=góc AEM = 90độ → tứ giác OAEM nội tiếp → 4 điểm O,A,E,M cùng nằm trên một đường tròn