a: Xét ΔBCE vuông tại C và ΔDBE vuông tại B có

góc E chung

Do đó: ΔBCE\(\sim\)ΔDBE

b: Đề sai rồi bạn

a)Ta có:

AO=BO=OC=DO (vì O là trung điểm của AC và BD)

AH=HI=IL=KL (vì H, I, K, L lần lượt là hình chiếu của O trên AB, BC, CD, DA)

AO=AH+HO

BO=HI+HO

CO=IL+HO

DO=KL+HO

AH+HO=HI+HO=IL+HO=KL+HO

AH=HI=IL=KL

Vậy, bốn đoạn thẳng AH, HI, IL, KL bằng nhau và có chung điểm cuối H. Do đó, bốn điểm H, I, K, L cùng nằm trên một đường tròn có tâm O.

b) Ta có:

AH=HI=IL=KL=AC/2

AO=BO=OC=DO=AC/2

Gọi r là bán kính của đường tròn (O).

Từ các kết quả trên, ta có:

r=AC/2=4cm/2=2cm

Vậy, bán kính của đường tròn (O) là 2cm.

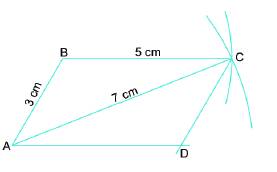
- Đặt một đầu compa tại điểm B đầu còn lại tại điểm C. Giữ nguyên compa và đặt một đầu tại điểm A, nếu đầu còn lại trùng với điểm D thì BC = AD.

- Đặt một đầu compa tại điểm B đầu còn lại tại điểm A. Giữ nguyên compa và đặt một đầu tại điểm C, nếu đầu còn lại trùng với điểm D thì AB = CD.

- Qua kiểm tra ta thấy BC = AD và AB = CD.

Học sinh tự vẽ hình

Sau khi đo, ta có: AC = BD = 5cm

Vậy : Hai đường chéo của hình chữ nhật dài bằng nhau

áp dụng định lý talet

a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có

góc E chung

=>ΔBDE đồng dạng với ΔDCE

b: Xét ΔHDC vuông tại H và ΔDBE vuông tại D có

góc HDC=góc DBE

=>ΔHDC đồng dạng với ΔDBE

=>DH/DB=CH/DE

=>DH*DE=CB*CH=DC^2

c: DC^2=CH*DB

=>CH*10=8^2=64

=>CH=6,4cm

\(DH=\sqrt{8^2-6.4^2}=4.8\left(cm\right)\)

=>DE=8^2/4,8=40/3(cm)

=>CE=32/3(cm)

Xét ΔHCE vuông tại H và ΔCDE vuông tại C có

góc HEC chung

=>ΔHCE đồng dạng với ΔCDE

=>\(\dfrac{S_{HCE}}{S_{CDE}}=\left(\dfrac{CE}{DE}\right)^2=\left(\dfrac{32}{3}:\dfrac{40}{3}\right)^2=\left(\dfrac{4}{5}\right)^2=\dfrac{16}{25}\)