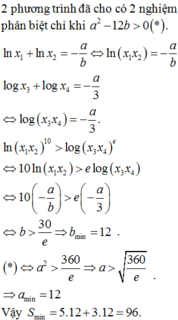xét các số nguyên x1;x2;...;x5 thỏa mãn (1 + x1)(1 + x2)···(1 + x5) = (1−x1)(1−x2)···(1−x5) = x. chứng minh rằng xx1x2...x5=0

Những câu hỏi liên quan
Xét tích A = x1 . x2 . x3 .... x30 trong đó x1 ; x2 ; ... x30 là 30 số nguyên dương tổng bằng 2003
Tìm max A
Xét các số nguyên dương a,b sao cho phương trình
b
ln
2
x
+
a
ln
x
+
3
0
có hai nghiệm phân biệt
x
1
,
x
2
và phương trình
3
log
2
x
+
a
log
x
+
b
0
có hai nghiệ...
Đọc tiếp
Xét các số nguyên dương a,b sao cho phương trình b ln 2 x + a ln x + 3 = 0 có hai nghiệm phân biệt x 1 , x 2 và phương trình 3 log 2 x + a log x + b = 0 có hai nghiệm phân biệt x 3 , x 4 thỏa mãn ln x 1 x 2 10 > log x 3 x 4 6 Tính giá trị nhỏ nhất của S=5a + 3b
A. 102
B. 101
C. 96
D. 99
Xét các số nguyên dương a,b sao cho phương trình
a
ln
2
x
+
b
ln
x
+
5
0
có hai nghiệm phân biệt
x
1
;
x
2
và phương trình
5
log
2
x
+...
Đọc tiếp
Xét các số nguyên dương a,b sao cho phương trình a ln 2 x + b ln x + 5 = 0 có hai nghiệm phân biệt x 1 ; x 2 và phương trình 5 log 2 x + b log x + a = 0 có hai nghiệm phân biệt x 3 ; x 4 thỏa mãn x 1 x 2 > x 3 x 4 . Tìm giá trị nhỏ nhất S m i n của S = 2a+3b.
A. Smin = 25
B. Smin = 17
C. Smin = 30
D. Smin = 33
Cho cấu hình của nguyên tử các nguyên tố
X
1
,
X
2
,
X
3
,
X
4
,
X
5
:
X
1
:
1
s
2
;
X...
Đọc tiếp
Cho cấu hình của nguyên tử các nguyên tố X 1 , X 2 , X 3 , X 4 , X 5 :
X 1 : 1 s 2 ;
X 2 : 1 s 2 2 s 1 ;
X 3 : 1 s 2 2 s 2 2 p 6 3 s 2 3 p 3 ;
X 4 : 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 4 s 2 ;
X 5 : 1 s 2 2 s 2 2 p 6 3 s 2 3 p 6 3 d 7 4 s 2 ;
Trong các nguyên tố cho ở trên, số các nguyên tố kim loại là
A. 2
B. 3
C. 4
D. 5
Nguyên tố X có 2 đồng vị X1 và X2. Đồng vị X1 có tổng số hạt là 18. Đồng vị X2 có tổng số hạt là 20. Biết rằng phần trăm các đồng vị như nhau, các loại hạt trong X1 bằng nhau. Nguyên tử khối trung bình của X là: A. 15 B. 14 C. 12 D. ĐA khác
Đọc tiếp
Nguyên tố X có 2 đồng vị X1 và X2. Đồng vị X1 có tổng số hạt là 18. Đồng vị X2 có tổng số hạt là 20. Biết rằng phần trăm các đồng vị như nhau, các loại hạt trong X1 bằng nhau. Nguyên tử khối trung bình của X là:
A. 15
B. 14
C. 12
D. ĐA khác
Vì phần trăm các đồng vị bằng nhau nên mỗi đồng vị chiếm 50%.
Vì các loại hạt trong X1 bằng nhau và X1 có tổng số hạt (gồm p, n, e) là 18
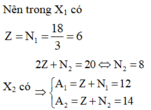
Vậy nguyên tử khối trung bình của X là:
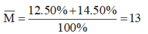
Đáp án D
Đúng 0
Bình luận (0)
Nguyên tố X có 2 đồng vị X1 và X2. Đồng vị X1 có tổng số hạt là 18. Đồng vị X2 có tổng số hạt là 20. Biết rằng % các đồng vị bằng nhau và các loại hạt trong X1 cũng bằng nhau. Nguyên tử khối trung bình của X là:
A. 15
B. 14
C. 12
D. 13
Đáp án D.
X1 có tổng các loại hạt bằng = 18 và các hạt trong X1 bằng nhau
Ta có p + e + n = 18 mặt khác p = e =n
=> p = e = n =6
X2 có số hạt proton bằng số hạt proton trong X1 do cùng là đồng vị:
2p + n =20 => n = 8
Ta có số khối của X1 = 12, X2 = 14 và %X1 = %X2 = 50%.
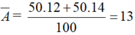
Đúng 0
Bình luận (0)
Nguyên tố X có 2 đồng vị X1 và X2. Đồng vị X1 có tổng số hạt là 18. Đồng vị X2 có tổng số hạt là 20. Biết rằng phần trăm các đồng vị như nhau, các loại hạt trong X1 bằng nhau. Nguyên tử khối trung bình của X là: A. 15 B. 14 C. 12 D. ĐA khác
Đọc tiếp
Nguyên tố X có 2 đồng vị X1 và X2. Đồng vị X1 có tổng số hạt là 18. Đồng vị X2 có tổng số hạt là 20. Biết rằng phần trăm các đồng vị như nhau, các loại hạt trong X1 bằng nhau. Nguyên tử khối trung bình của X là:
A. 15
B. 14
C. 12
D. ĐA khác
Đáp án D
Vì phần trăm các đồng vị bằng nhau nên mỗi đồng vị chiếm 50%.
Vì các loại hạt trong X1 bằng nhau và X1 có tổng số hạt (gồm p, n, e) là 18
Nên trong X1 có Z = N 1 = 18 3 = 6
X2 có 2 Z + N 2 = 20 ⇔ N 2 = 8 ⇒ A 1 = Z + N 1 = 12 A 2 = Z + N 2 = 14
Vậy nguyên tử khối trung bình của X là:
M
¯
=
12
.
50
%
+
14
.
50
%
100
%
=
13
Đúng 0
Bình luận (0)
Viết chương trình tính và in ra tổng các số nguyên chia hết cho 3 trong dãy số nguyên X1, X2, X3, ...Xn biết dãy số X1, X2, X3, ... Xn được nhập từ bàn phím
var n:integer;
begin
write('Nhap n: '); readln(n);
if (n mod 3 =0) then
write(n,' chia het cho 3')
else
write(m,' k chia het cho 3');
readln;
end.
Đúng 0
Bình luận (0)
#include <bits/stdc++.h>
using namespace std;
long long x,n,i,t;
int main()
{
cin>>n;
t=0;
for (i=1;i<=n; i++)
{
cin>>x;
if (x%3==0) t+=x;
}
cout<<t;
return 0;
}
Đúng 0
Bình luận (0)
Một nguyên tố X gồm 2 đồng vị X1 và X2. Đồng vị X1 có tổng số hạt là 18. Đồng vị X2 có tổng số hạt là 20. Biết rằng phần trăm các đồng vị trong X bằng nhau và các loại hạt trong X1 cũng bằng nhau. Nguyên tử khối trung bình của X là A. 12. B. 12,5. C. 13. D. 14.
Đọc tiếp
Một nguyên tố X gồm 2 đồng vị X1 và X2. Đồng vị X1 có tổng số hạt là 18. Đồng vị X2 có tổng số hạt là 20. Biết rằng phần trăm các đồng vị trong X bằng nhau và các loại hạt trong X1 cũng bằng nhau. Nguyên tử khối trung bình của X là
A. 12.
B. 12,5.
C. 13.
D. 14.
Đáp án C
Đồng vị X1 có tổng số hạt là 18 → 2Z1 + N1 = 18
Trong X1 có các loại hạt bằng nhau
→ Z1= N1 =
18
3
= 6 → A1 = Z1 + N1 = 12
Đồng vị X2 có tổng số hạt là 20
→ 2Z2 + N2 = 20
Luôn có Z2=Z1 ( cùng là đồng vị của nguyên tố X)
→ Z2 = 6 → N2 = 8 → A2 = 6 + 8 = 14
Nguyên tử khối trung bình của X là
M X = ( 50 . 12 + 20 . 14 ) / 100 = 13
Đúng 0
Bình luận (0)