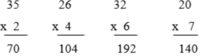\(96x^2-208x-132xy+148y+45y^2+96.\)

\(=\left(45y^2-60xy+40y\right)+\left(-72xy+96x^2-64x\right)+\left(108y-144x+96\right)\)

\(=5y\left(9y-12x+8\right)-8x\left(9y-12x+8\right)+12\left(9y-12x+8\right)\)

\(=\left(9y-12x+8\right)\left(5y-8x+12\right)\)

a) y 2   –   4 xy 2   +   4 x 2 y 2 .                 b) x 2 − 32 5 xy + 256 25 y 2 .  

c) 1 9 a 2 b 4 − c 6 .                             d) a 4 − 8 9 a + 16 81 .

\(35x^2-49=10x^2< =>25x^2-7^2=0\)

\(< =>\left(5x\right)^2-7^2=0< =>\left(5x+7\right)\left(5x-7\right)=0\)

\(=>\left[{}\begin{matrix}x=-\dfrac{7}{5}\\x=\dfrac{7}{5}\end{matrix}\right.\)

Ta có: \(35x^2-49=10x^2\)

\(\Leftrightarrow25x^2-49=0\)

\(\Leftrightarrow\left(5x-7\right)\left(5x+7\right)=0\)

\(\Leftrightarrow x\in\left\{\dfrac{7}{5};-\dfrac{7}{5}\right\}\)

Đáp án D.

∫ 3 5 x 2 + x + 1 x + 1 d x = ∫ 3 5 x + 1 x + 1 d x = x 2 2 + ln x + 1 5 3 = 8 + ln 3 2 ⇒ a = 8 b = 3 ⇒ S = a − 2 b = 2

a) Kết quả - 2 x 4   +   3 x 2  + 5.          b) Kết quả - 4 x 3   + 1 2 x − 1.

a: \(x^2-4xy+4y^2-2x+4y-35\)

\(=\left(x^2-4xy+4y^2\right)-\left(2x-4y\right)-35\)

\(=\left(x-2y\right)^2-2\left(x-2y\right)-35\)

\(=\left(x-2y\right)^2-7\left(x-2y\right)+5\left(x-2y\right)-35\)

\(=\left(x-2y\right)\left(x-2y-7\right)+5\left(x-2y-7\right)\)

\(=\left(x-2y-7\right)\left(x-2y+5\right)\)

c: \(\left(xy+ab\right)^2+\left(ay-bx\right)^2\)

\(=x^2y^2+a^2b^2+2xyab+a^2y^2-2aybx+b^2x^2\)

\(=x^2y^2+a^2y^2+a^2b^2+b^2x^2\)

\(=y^2\left(x^2+a^2\right)+b^2\left(a^2+x^2\right)\)

\(=\left(x^2+a^2\right)\left(y^2+b^2\right)\)