Tìm các cặp số nguyên x,y biết :
a, xy=x+y
a,Tìm x thuộc z/|x|<18
b,Tìm xy thuộc z/|x-3|+|y-5|=0
c,Tìm các cặp số nguyên (xy)/|x|+|y|=4
d,Tìm các cặp số nguyên (xy)/|x|+|y|<hoặc=3
BÀi 1:Tìm các cặp số nguyên x,y biết 2x2+y2+xy=2(x+y)
Bài 2:Tìm các cặp số nguyên dương x,y biết x2+y2=3(x+y)
Bài 2: Giả sử tồn tại x,y nguyên dương t/m đề, khi đó pt cho tương đương:
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x+3\right)^2+\left(2y+3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x+3=3\\2y+3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=0\\y=0\end{cases}}\)
Vậy cặp nghiệm nguyên t/m pt là (x;y) = (0;0)
Làm lại bài 2 :v (P/S: Bạn bỏ bài kia đi nhé)
\(4x^2+4y^2-12x-12y=0\Leftrightarrow\left(2x-3\right)^2+\left(2y-3\right)^2=18\)
Ta thấy: \(18=9+9=3^2+3^2\). Mà x,y thuộc Z+ nên \(\hept{\begin{cases}2x-3=3\\2y-3=3\end{cases}\Leftrightarrow}\hept{\begin{cases}x=3\\y=3\end{cases}}\)
Vậy (x;y) = (3;3)
Tìm tất cả các cặp số nguyên (x,y) biết rằng a, (x + 3).(y - 2) = 7 b, (x + 1).(xy+2) = 5
a: \(\Leftrightarrow\left(x+3;y-2\right)\in\left\{\left(1;7\right);\left(7;1\right);\left(-1;-7\right);\left(-7;-1\right)\right\}\)
=>\(\left(x,y\right)\in\left\{\left(-2;9\right);\left(4;3\right);\left(-4;-5\right);\left(-10;1\right)\right\}\)
b: (x+1)(xy+2)=5
=>\(\left(x+1;xy+2\right)\in\left\{\left(1;5\right);\left(5;1\right);\left(-1;-5\right);\left(-5;-1\right)\right\}\)
=>\(\left(x,xy\right)\in\left\{\left(0;3\right);\left(4;-1\right);\left(-2;-7\right);\left(-6;-3\right)\right\}\)
mà x,y là số nguyên
nên (x,y)=\(\varnothing\)
Tìm các cặp số nguyên x, y biết
a, x. ( y - 3) = - 4
b, xy - 3x - y = 0
c, xy + 2x + 2y = -16
Tìm các cặp số nguyên x, y biết: x y = 2 7
Áp dụng Tính chất cơ bản của phân số: Nếu ta nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số mới bằng phân số đã cho:
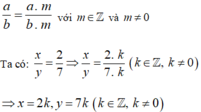
tìm các cặp số nguyên (x,y) biết : 2x+xy+y=1
2x + xy + y = 1
=> x(2 + y) + y + 2 = 1 + 2
=> x(y + 2) + 1(y + 2) = 3
=> (x + 1)(y + 2) = 3
=> x + 1 và y + 2 thuộc Ư(3) = {-1; 1; -3; 3}
ta có bảng :
| x+1 | -1 | 1 | -3 | 3 |
| y+2 | -3 | 3 | -1 | 1 |
| x | -2 | 0 | -4 | 2 |
| y | -5 | 1 | -3 | -1 |
Tìm tất cả các cặp số nguyên (x;y) biết x, y thoả mãn |xy|+|x-y|=1. Giải thích?
Tìm các cặp số nguyên x,y biết:
xy-2x+y=3
3x-xy-y=1
xy - 2x + y = 3
=> x ( y - 2) + ( y - 2 ) = 3 - 2
=> ( x + 1 ) ( y - 2 ) = 1
=> x + 1 và y - 2 thuộc Ư(1) = { 1; -1 }
Lập bảng:
x + 1 | 1 | -1 |
x | 0 | -2 |
y - 2 | -1 | 1 |
y | 1 | 3 |
Vậy x=0 , y=-2 hoặc x=1 , y=3
\(\text{xy - 2x + y = 3}\)
\(\text{\Rightarrow x ( y - 2) + ( y - 2 ) = 3 - 2}\)
\(\text{\Rightarrow( x + 1 ) ( y - 2 ) = 1}\)
=> \(\text{x + 1}\) và \(\text{y - 2}\) thuộc \(Ư_{\left(1\right)}\in\left\{\pm1\right\}\)
Lập bảng:
| \(x+1\) | \(1\) | \(-1\) |
| \(x\) | \(0\) | \(-2\) |
| \(y-2\) | \(-1\) | \(1\) |
| \(y\) | \(1\) | \(3\) |
Vậy \(\left(x;y\right)\in\left\{\left(0;-2\right);\left(1;3\right)\right\}\)
a) Ta có: xy - 2x +y = 3
x( y-2) +( y-2)= 3-2
(x+1)(y-2)=1=1.1= -1.(-1)
Ta có bảng sau
| x+1 | 1 | -1 |
| y-2 | 1 | -1 |
| x | 0 | -2 |
y | 3 | 1 |
Tìm các cặp số nguyên x,y biết
a)x . (y - 3) = -12
b)xy - 3x - y=0
c)xy + 2x + 2y=-16