Cho hình thoi ABCD có Â=40 độ. Tính các góc còn lại của hình thoi ABCD ?

Những câu hỏi liên quan
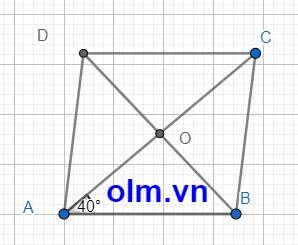
Bài 13: Cho hình thoi ABCD, biết O là giao điểm của hai đường chéo và góc BAO40 độ
a) Tính góc BAD
b) Tính các góc còn lại của hình thoi.
Đọc tiếp
Bài 13: Cho hình thoi ABCD, biết O là giao điểm của hai đường chéo và góc BAO=40 độ
a) Tính góc BAD
b) Tính các góc còn lại của hình thoi.
Vì ABCD là hình thoi nên ⇒ tam giác ABD cân tại A
Vì O là trung điểm DB nên AO là truyến là đường phân giác của tam giác ABD
⇒ \(\widehat{DAO}\) = 400
⇒ \(\widehat{DAB}\) = 400 + 400 = 1800
⇒ \(\widehat{ADC}\) = 1800 - 800 = 1000
⇒ \(\widehat{DCB}\) = 1800 - 1000 = 800
\(\Rightarrow\) \(\widehat{ABC}\) = 1800 - 800 = 1000
Đúng 1
Bình luận (0)
cho hình thoi ABCD có góc A bằng 90* tính số đo các góc còn lại của hình thoi
Cho hình thoi ABCD có góc A=60 độ, AB=10cm. Tính diện tích hình thoi ABCD.
Kẻ BH vuông góc AD
Tam giác ABH là tam giác đều nên BH=AD=10(cm)
Suy ra SABCD=10.10=100(cm2)
Cho hình thoi ABCD có diện tích bằng 50√3cm^2 và AC=10cm
1/ Tính độ dài BD và AB
2/ Tính số đo các góc của hình thoi ABCD
Giúp em câu 2 với ạ, em cảm ơn.
1) \(S_{ABCD}=\dfrac{1}{2}.AC.BD\Rightarrow BD=\dfrac{2S_{ABCD}}{AC}=\dfrac{2.50\sqrt[]{3}}{10}=10\sqrt[]{3}\left(cm\right)\)
Gọi O là giao điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}OA=\dfrac{1}{2}AC=5\left(cm\right)\\OB=\dfrac{1}{2}BD=5\sqrt[]{3}\left(cm\right)\end{matrix}\right.\)
Xét Δ vuông OAB có :
\(AB^2=OA^2+OC^2=25+25.3=100\left(cm^2\right)\left(Pitago\right)\)
\(\Rightarrow AB=10\left(cm\right)\)
2) Xét Δ vuông OAB có :
\(AB=2OA=10\left(cm\right)\)
⇒ Δ OAB là Δ nửa đều
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABD}=30^o\\\widehat{BAC}=60^o\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2\widehat{BAC}\\\widehat{ADC}=\widehat{ABC}=2\widehat{ABD}\end{matrix}\right.\) (tính chất hình thoi)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2.60=120^o\\\widehat{ADC}=\widehat{ABC}=2.30=60^o\end{matrix}\right.\)
Đúng 3
Bình luận (0)
Cho hình thoi abcd có góc c bằng 45 độ. Đường chéo ac bằng 8 cm. Hỏi tính diện tích hình thoi abcd?
Cho hình thoi ABCD có diện tích bằng 50 căn 3cm^2 và AC=10cm.
1) Tính độ dài BD và AB
2) Tính số đo các góc của hình thoi ABCD
Trong hệ tọa độ Oxy, cho hình thoi ABCD có đỉnh D(1;-5), trung điểm cạnh AB, AC lần lượt là M(2;-3) và N(3;-4). Tìm tọa độ các đỉnh còn lại của hình thoi.
có hình ko bạn..Đề này quen quen, hình như mình làm rồi.
Đúng 0
Bình luận (0)
Cho hình thoi ABCD, có B=40 độ, E là trung điểm BC, Hạ AF vuông góc DE. TÍnh góc DFC
cho hình thang ABCD có 2 duong92 cao AH,AK
a, CMR AH=AK
b,Biết góc B=60 độ. tam giác AHK là tam giác gì? vì sao?
c, Biết hình thoi ABCD có chu vi=16cm,Ah=2cm tính các góc của hình thoi














