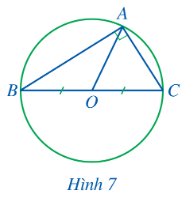
Cho tam giác ABC vuông tại A. Gọi O là trung điểm của BC (hình 7). Đường tròn (O; OB) có phải là đường tròn ngoại tiếp tam giác ABC hay không?
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Gọi P, Q, K lần lượt là trung điểm của ba cạnh AB, AC, BC. Gọi O là giao điểm của ba đường phân giác của tam giác ABC. Khỉ đó tâm đường tròn ngoại tiếp tam giác ABC là:
A. O.
B. P.
C. Q.
D. R.
Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt trung điểm của AB, AC và BC. Gọi O là giao điểm của ba đường phân giác trong tam giác ABC. Khi đó, tâm đường tròn ngoại tiếp tam giác ABC là:
A. O
B. D
C. E
D. F
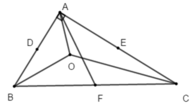
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D
Đúng 0
Bình luận (0)
14 tháng 1 2022 lúc 16:27
Cho tam giác ABC vuông tại A . Đường tròn (O) đường kính AB cắt BC tại H . Tia phân giác của góc HAC cắt DC tại E và cắt đường tròn (O) tại B .
a) Chứng minh: AH\(\perp BC\)
b) Gọi M là trung điểm của AB . Chứng minh HM là tiếp tuyến của đường tròn tâm O
c) Chứng minh: DA. DE=DC\(^2\)
a: Xét (O) có
ΔAHB nội tiếp
AB là đường kính
Do đó: ΔAHB vuông tại H
hay AH⊥BC
b: Sửa đề: M là trung điểm của AC
Ta có: ΔAHC vuông tại H
mà HM là đường trung tuyến
nên HM=AM=AC/2
Xét ΔMAO và ΔMHO có
MA=MH
MO chung
OA=OH
Do đó: ΔMAO=ΔMHO
Suy ra: \(\widehat{MAO}=\widehat{MHO}=90^0\)
hay HM là tiếp tuyến của (O)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A và AB AC. Từ A, kẻ AH vuông góc với cạnh BC tại H. Trên đoạn thẳng HC lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Gọi O là trung điểm của đoạn thẳng CD, vẽ đường tròn tâm O đường kính CD. Đường tròn (O) vừa vẽ có điểm chung thứ hai với cạnh AC là E. Chứng minh HA HE và tính số đo của góc OEH. Giúp mình với mình đang cần gấp lắm ạ
Đọc tiếp
Cho tam giác ABC vuông tại A và AB < AC. Từ A, kẻ AH vuông góc với cạnh BC tại H. Trên đoạn thẳng HC lấy điểm D sao cho H là trung điểm của đoạn thẳng BD. Gọi O là trung điểm của đoạn thẳng CD, vẽ đường tròn tâm O đường kính CD. Đường tròn (O) vừa vẽ có điểm chung thứ hai với cạnh AC là E. Chứng minh HA = HE và tính số đo của góc OEH.
Giúp mình với mình đang cần gấp lắm ạ
Bài 6. (2,5 điểm) Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AB cắt BC tại H. Gọi I là trung điểm AH, BI cắt đường tròn (O) tại E. Tia AE cắt BC tại K. a) Chứng minh tam giác ABH vuông tại H và KI vuông góc với AB. b) Chứng minh: tan ABK . tan AKB = 2. c) Đường thẳng qua H và song song với AC cắt AK tại M. Chứng minh: MC là tiếp tuyến đường tròn ngoại tiếp Tam giác ABC.
Cho đường tròn O, đường kính AB. Lấy C thuộc (O) (C khác A và B). Tiếp tuyến tại A của đường tròn O cắt BC tại M.
a, CM: tam giác ABC vuông và BA2=BC.BM b, Gọi K là trung điểm của MA. CM:KC là tiếp tuyến của đường tròn O
a: Xét (O) có
ΔABC nội tiếp đường tròn
AB là đường kính
Do đó: ΔACB vuông tại C
Xét ΔBAM vuông tại A có AC là đường cao ứng với cạnh huyền MB
nên \(BA^2=BC\cdot BM\)
Đúng 4
Bình luận (0)
cho tam giác ABC vuông tại A. Vẽ các đường tròn O và i đi qua A và tiếp xúc với BC tại các điểm B và C. Gọi M là trung điểm của BC. Chứng Minh
a) Các đường tròn O và i tiếp xúc với nhau
b) AM là tiếp tuyến chung của hai đường tròn O và i
c) tam giác OMI vuông
d) BC là tiếp tuyến của đường tròn ngoại tiếp tam giác OMI.
Cho tam giác cân ABC ( AB = AC) nội tiếp đường tròn (O). Gọi D là trung điểm của AC; tiếp tuyến của đường tròn (O) tại A cắt tia BD tại E. Tia CE cắt (O) tại F.
1.Chứng minh BC // AE.
2.Chứng minh ABCE là hình bình hành.
3.Gọi I là trung điểm của CF và G là giao điểm của BC và OI. So sánh góc BAC và BGO.
Xem chi tiết
1) Xét (O) có
ΔABC nội tiếp đường tròn(gt)
nên O là giao điểm ba đường trung trực của ΔABC
hay AO là đường trung trực của BC
⇒AO⊥BC
Ta có: AO⊥BC(cmt)
AO⊥AE(AE là tiếp tuyến có A là tiếp điểm của (O))
Do đó: AE//BC(Định lí 1 từ vuông góc tới song song)
2) Xét ΔADE và ΔCDB có
\(\widehat{ADE}=\widehat{CDB}\)(hai góc đối đỉnh)
DA=DC(D là trung điểm của AC)
\(\widehat{DAE}=\widehat{DCB}\)(hai góc so le trong, AE//BC)
Do đó: ΔADE=ΔCDB(c-g-c)
⇒AE=CB(hai cạnh tương ứng)
Xét tứ giác ABCE có
AE//CB(cmt)
AE=CB(cmt)
Do đó: ABCE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Đúng 1
Bình luận (0)
Cho đường tròn ( I ), ( O ) nội tiếp , ngoại tiếp tam giác ABC . AI cắt ( O ) tại D .
a, Tam giác BDI là tam giác gì ?
b, Gọi M là trung điểm của BC . Kẻ AH vuông góc với BC . Gọi K là giao điểm của AH , MI . Chứng minh AK = r , r là bán kính của đường tròn tâm I .
Bài 5:Cho tam giác ABC vuông tại A, có AB 8 cm; AC 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.a)Tính độ dài đoạn BC và AMb)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.c) Chứng minh tứ giác OACE nội tiếp Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (MBC, NAC). Hai đường cao AM và BN cắt nhau tại H.a)Chứng minh rằng tứ giác CMHN nội tiếp một đường trònb)Chứng minh rằng AM.CH AC.MN
Đọc tiếp
Bài 5:Cho tam giác ABC vuông tại A, có AB = 8 cm; AC = 6 cm. Gọi O là trung điểm của AB, về đường tròn (O) tâm 0 đường kính AB; BC cắt đường tròn (O) tại điểm M.
a)Tính độ dài đoạn BC và AM
b)Từ C và tiếp tuyến với đường tròn (O) có tiếp điểm là E khác A.
c) Chứng minh tứ giác OACE nội tiếp
Bài 7: Cho tam giác ABC có ba góc nhọn, kẻ các đường cao AM và BN (M=BC, N=AC). Hai đường cao AM và BN cắt nhau tại H.
a)Chứng minh rằng tứ giác CMHN nội tiếp một đường tròn
b)Chứng minh rằng AM.CH = AC.MN
