Cho tam giác đều ABC (H.9.22).
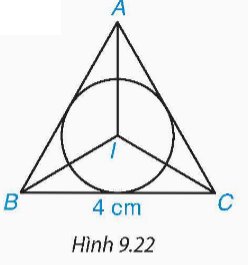
a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.
b) Biết rằng BC = 4 cm, hãy tính bán kính r.
Cho tam giác đều ABC cạnh a. vẽ đường tròn (O) có đường kính là đường cao AH của tam giác.Gọi (I) là đường tròn nội tiếp tam giác ABC. Tính diện tích phần chung của tam giác ABC với đường tròn (O) nhưng không thuộc đường tròn (I).áp dụng với a=căn bậc hai của 11.
a) Vẽ tam giác đều ABC cạnh a = 3cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O; R).
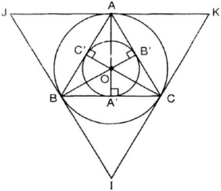
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).
+ Dựng đoạn thẳng AB = 3cm .
+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.
Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.
b) * Vẽ đường tròn:
Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.
Dựng đường trung trực của đoạn thẳng BC và CA.
Hai đường trung trực cắt nhau tại O.
Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.
* Tính bán kính đường tròn.
+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.
và AA’ ⊥ BC
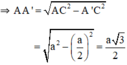
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến
=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến
Suy ra O là trọng tâm tam giác ABC.
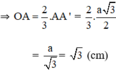
Vậy R = √3 (cm).
c) * Vẽ đường tròn:
Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc 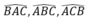
Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.
Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.
* Tính r:
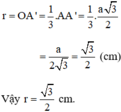
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).
a) Vẽ tam giác đều ABC cạnh a = 3 cm.
b) Vẽ tiếp đường tròn (O; R) ngoại tiếp tam giác đều ABC. Tính R.
c) Vẽ tiếp đường tròn (O; r) nội tiếp tam giác đều ABC. Tính r.
d) Vẽ tiếp tam giác đều IJK ngoại tiếp đường tròn (O ; R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).
cho tam giác ABC vẽ đường tròn đường kính BC . vẽ đường cao AK của tam giác từ A vẽ tiếp tuyến AM,ĂN với tròn đường tròn (O). MN cắt AK tại H. chứng minh H là trưc tâm tam giác ABC
Bài 1: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Đường tròn (I) qua A và tiếp xúc với BC tại B. Đường tròn (K) qua A và tiếp xúc với BC tại C. Các đường tròn (I) và(K) cắt tại M. Đường thẳng AM cắt đường tròn (O) tại N. C/m: BMCN là hình bình hành
Bài 2: Cho tam giác đều ABC nội tiếp đường tròn (O). Trên cung nhỏ BC lấy điểm M và vẽ đường tròn (I) tiếp xúc trong với (O) tại M. Gọi giao điểm MA, MB, MC với (I) theo tứ tự D,E,F
a) C/m: tam giác DEF đều.
b) Từ A,B,C vẽ các tiếp tuyến với đường tròn (I) lần lượt là AP,BQ,CR( P,Q,R là tiếp điểm). C/m: AP=PQ+CR
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC) Vẽ (A;AH) vẽ đường kính HD.Qua D vẽ tiếp tuyến với đường tròn,tiếp tuyến này cắt BA kéo dài tại điểm E
a)CMR: tam giác ADE=tam giác AHB
b)tam giác CBE cân
c) Gọi I là hình chiếu của A trên CE.CMR:CE là tiếp tuyến của đường tròn (A;AH)
hình bạn tự kẻ nha
a> Xét tam giác ADE và tam giác AHB có : góc DAE = HAB(đối đỉnh); góc ADE = góc AHB = 90 độ; AD = AH = bán kính==> tg ADE = AHB (c.g.v_g.n.k)
b> vì tg ADE = AHB ==> AE = AB ==> A là trung điểm của BE (1)
xét tg CBE ta thấy CA vuông góc với AB ==> CA là đường cao (2)
từ (1) và (2) ==> tg CBE cân tại C
c> vì tg CBE cân tại C ==> CA vừa là đường cao vừa là tia pg xuất phát từ đỉnh C ==> góc ACH = ACI
xét tg ACH và tg ACI có: góc AHC = AIC = 90 độ; AC là cạnh chung; góc ACH = ACI(cmt) ==> tg ACH = ACI (c.h_g.n)
=> AH=AI=bán kính (3)
mặt khác AI vuông góc với CE (4)
từ (3) và (4) ==> CE là tiếp tuyến ( khoảng cách từ tâm đến đường thẳng bằng bán kính)
Cho tam giác ABC vuông ở A, điểm I trên cạnh AC. Vẽ đường tròn đường kính IC cắt BC ở E, cắt BI ở D (D khác I). Chứng minh:
a)4 điểm A, B, C, D cùng nằm trên một đường tròn; 4 điểm A, B, E, I cùng nằm trên một đường tròn.
b) I cách đều 3 cạnh của tam giác ADE
c) 3 đường thẳng AB, CD, EI đồng qui
Mn ơi giúp e với =')
Giữ lời hứa 1 câu trl 3 coin
Tổng cộng mốt e đủ coin thì e đưa cj 6 coin , h cj cho khất nợ:)
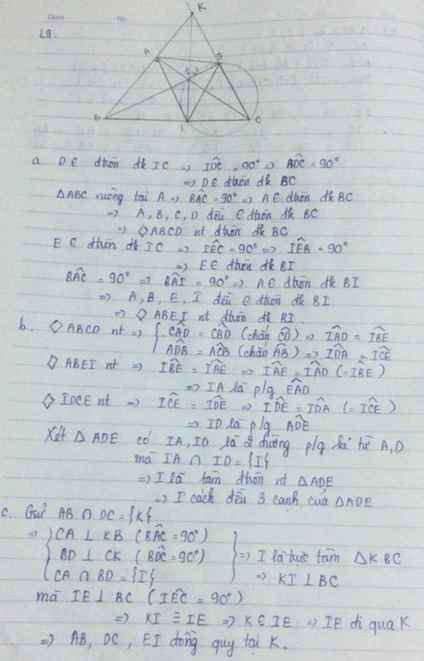
Cho tam giác ABC đều nội tiếp đường tròn (O;R). Vẽ đường tròn (I) tiếp xúc với AB, AC và tiép xúc trong với (O). Tính IB theo R
minh moi bn vao link nay dang ky roi tra loi minigame nha : https://alfazi.edu.vn/question/5b7768199c9d707fe5722878
Gọi tiếp điểm của đường tròn (I) với AB và (O;R) theo thứ tự là D và E.
Đường tròn (I) tiếp xúc trong với (O;R) tại E nên 4 điểm A;O;I;E thẳng hàng.
Ta có: AO là phân giác của ^BAC (Do \(\Delta\)ABC đều nội tiếp (O))
=> AI là phân giác ^BAC => ^DAI = ^BAC / 2 = 300
AB tiếp xúc với (I) tại D => ^ADI = 900.
Xét \(\Delta\)AID có: ^ADI = 900; ^DAI = 300 => \(\Delta\)AID nửa đều \(\Rightarrow\frac{ID}{AI}=\frac{1}{2}\)
Hay \(\frac{IE}{AI}=\frac{1}{2}\Rightarrow\frac{IE}{AE}=\frac{1}{3}\)(Do A;I;E thẳng hàng) \(\Rightarrow IE=ID=\frac{2R}{3}\)
Thấy ^ABE chắn nửa đg tròn (O;R) => ^ABE = 900 => BE vuông góc AB. Mà ID vuông góc AB
=> ID // BE => \(\frac{IE}{AE}=\frac{BD}{AB}=\frac{1}{3}\)(Theo ĐL Thales)
Áp dụng ĐL Pytagorean ta dễ dàng tính được: \(AB=R.\sqrt{3}\)\(\Rightarrow BD=\frac{AB}{3}=\frac{R}{\sqrt{3}}\)
Trong \(\Delta\)BDI có ^IDB = 900 . Áp dụng ĐL Pytagorean:
\(IB=\sqrt{BD^2+ID^2}=\sqrt{\frac{R^2}{3}+\frac{4R^2}{9}}=\sqrt{\frac{7R^2}{9}}=\frac{R.\sqrt{7}}{3}\)
ĐS: .....
cho đường tròn tam o ban kính r có đường kính AI.Gọi H là trung điểm của OI .Vẽ dây cung BC vuông góc với OI tại H .Chứng minh tam giác ABC đều
Cho đường tròn (O;R) và 1 điểm A cách O 1 khoảng 2R. Từ A vẽ các tiếp tuyến AB,AC với đường tròn (B,C là các tiếp điểm)
a) Cm: OA là đường trung trực của BC
b) Gọi H là giao điểm của OA và BC. Cm: HA.HO=HB.HC
c)Cm: tam giác ABC đều. Tính cạnh AB theo R
d) OA cắt đường tròn (O) tại I. Cm: I là tâm đường tròn nội tiếp tam giác
Giúp mình giải câu d nhé !!!!!!!!!!!!!