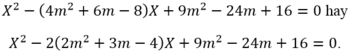Chọn B

bạn đăng tách ra cho mn giúp nhé 

a, Để pt có 2 nghiệm pb 

\(\Delta'=1-m\ge0\Leftrightarrow m\le1\)

Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=-2\left(1\right)\\x_1x_2=m\left(2\right)\end{matrix}\right.\)

\(x_1-3x_2=0\)(3) 

Từ (1) ; (3) ta có hệ \(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1-3x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_1=-2\\x_2=-2-x_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=-\dfrac{3}{2}\end{matrix}\right.\)

Thay vào (2) ta được \(m=\left(-\dfrac{1}{2}\right)\left(-\dfrac{3}{2}\right)=\dfrac{3}{4}\)

\(b,\Delta=\left(m+5\right)^2-4\left(-m+6\right)\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-7-4\sqrt{3}\\m\ge-7+4\sqrt{3}\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x1+x2=m+5\\2x1+3x2=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x1+2x2=2m+10\\2x1+3x2=13\end{matrix}\right.\)\(\)

\(\Rightarrow x2=13-2m-10=3-2m\Rightarrow x1=m+5-x2=m+5-3+2m=3m+2\)

\(x1x2=6-m\Rightarrow\left(3-2m\right)\left(3m+2\right)=6-m\Leftrightarrow\left[{}\begin{matrix}m=0\left(tm\right)\\m=1\left(tm\right)\end{matrix}\right.\)

\(c,\Delta'=\left(m+1\right)^2-\left(m^2-2m+29\right)\ge0\Leftrightarrow m\ge7\)

\(\Rightarrow\left\{{}\begin{matrix}x1+x2=2m+2\\x1=2x2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x2=\dfrac{2m+2}{3}\\x1=\dfrac{2\left(2m+2\right)}{3}\end{matrix}\right.\)

\(\Rightarrow x1.x2=\dfrac{\left(2m+2\right).2\left(2m+2\right)}{9}=m^2-2m+29\Leftrightarrow\left[{}\begin{matrix}m=11\left(tm\right)\\m=23\left(tm\right)\end{matrix}\right.\)

Giả sử  x 1 ,   x 2  là hai nghiệm của phương trình bậc hai a x 2  + bx + c = 0 có ∆’ = 0

Do đó, phương trình có nghiệm kép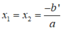 

Chọn B

Đáp án A

Giả sử  x 1 ,  x 2  la hai nghiệm của phương trình  x 2 + px + q = 0

Theo hệ thức Vi-ét ta có:  x 1 +  x 2  = - p/1 = - p;  x 1 x 2  = q/1 = q

Phương trình có hai nghiệm là  x 1  +  x 2  và  x 1 x 2  tức là phương trình có hai nghiệm là –p và q.

Hai số -p và q là nghiệm của phương trình.

(x + p)(x - q) = 0 ⇔  x 2  - qx + px - pq = 0 ⇔  x 2  + (p - q)x - pq = 0

Phương trình cần tìm:  x 2  + (p - q)x - pq = 0

Gọi nghiệm của phương trình (2) là x₀ (x₀ ≠ 0)

thì nghiệm phương trình (1) là 2x₀

Thay x₀; 2x₀ lần lượt vào phương trình (2) và (1)

ta được

2 x 0 2 − 13.2 x 0 + 2 m = 0 x 0 2 − 4 x 0 + m = 0

⇔ 4 x 0 2 − 26 x 0 + 2 m = 0 x 0 2 − 4 x 0 + m = 0 ⇔ 4 x 0 2 − 26 x 0 + 2 m = 0 4 x 0 2 − 16 x 0 + 4 m = 0

⇔ 10x₀ = −2m ⇔ x 0 = − m 5

Do x₀ ≠ 0 nên m ≠ 0

Thay x 0 = − m 5 vào phương trình (2)

ta được − m 5 2 − 4. − m 5 + m = 0

⇔ m 2 25 + 4 m 5 + m = 0

⇔ m 2 25 + 9 m 5 = 0 ⇒ m = 0 m = − 45

Kết hợp m ≠ 0 ta được m = −45

Đáp án cần chọn là: A

a)  2 x 2   –   17 x   +   1   =   0

Có a = 2; b = -17; c = 1

Δ   =   b 2   –   4 a c   =   ( - 17 ) 2   –   4 . 2 . 1   =   281   >   0 .

Theo hệ thức Vi-et: phương trình có hai nghiệm x1; x2 thỏa mãn:

x 1 + x 2 = − b / a = 17 / 2 x 1 x 2 = c / a = 1 / 2

b)  5 x 2   –   x   –   35   =   0

Có a = 5 ; b = -1 ; c = -35 ;

Δ   =   b 2   –   4 a c   =   ( - 1 ) 2   –   4 . 5 . ( - 35 )   =   701   >   0

Theo hệ thức Vi-et, phương trình có hai nghiệm x1; x2 thỏa mãn:

x 1 + x 2 = − b / a = 1 / 5 x 1 ⋅ x 2 = c / a = − 35 / 5 = − 7

c)  8 x 2   –   x   +   1   =   0

Có a = 8 ; b = -1 ; c = 1

Δ   =   b 2   –   4 a c   =   ( - 1 ) 2   –   4 . 8 . 1   =   - 31   <   0

Phương trình vô nghiệm nên không tồn tại x1 ; x2.

d)  25 x 2   +   10 x   +   1   =   0

Có a = 25 ; b = 10 ; c = 1

Δ   =   b 2   –   4 a c   =   10 2   –   4 . 25 . 1   =   0

Khi đó theo hệ thức Vi-et có:

x 1 + x 2 = − b / a = − 10 / 25 = − 2 / 5 x 1 x 2 = c / a = 1 / 25

Hai số 2 và 5 là nghiệm của phương trình :

(x – 2)(x – 5) = 0 ⇔  x 2  – 7x + 10 = 0

Hai số 0,1 và 0,2 là nghiệm của phương trình :

(x – 0,1)(x – 0,2) = 0 ⇔  x 2  – 0,3x + 0,02 = 0

Đáp án: D

Theo định lý Vi-ét ta có

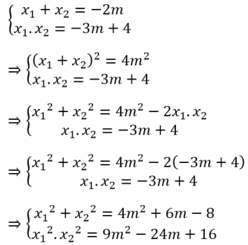
Khi đó,   là nghiệm của phương trình