Cho một hình vuông có độ dài mỗi cạnh bằng 6 cm và hai đường chéo cắt nhau tại I. Chứng minh rằng đường tròn (I; 3 cm) tiếp xúc với cả bốn cạnh của hình vuông.

Những câu hỏi liên quan
Cho hình vuông ABCD có độ dài cạnh bằng 4 cm. Tia phân giác của góc ACB cắt cạnh AB tạii M. Vẽ đường tròn đươngf kính CM, Đường tròn này cắt đường chéo AC tạii điểm E E khác C . Tia ME cắt cạnh AD tại điểm N tia CN cắt đường tròn đường kính CM tại điểm I I khác C .a Chứng minh tam giác CBM bằng tam giác CEM và tam giác CEN bằng tam giác CDN , từ đó suy ra CN là tia phân giác của góc ACD.b Chứng minh hệ thức AM2 AN2 BM DN 2.c Chứng minh rằng 3 điểm B, I, D thẳng hàng.d Tính diện tích của tam giác...
Đọc tiếp
Cho hình vuông ABCD có độ dài cạnh bằng 4 cm. Tia phân giác của góc ACB cắt cạnh AB tạii M. Vẽ đường tròn đươngf kính CM, Đường tròn này cắt đường chéo AC tạii điểm E E khác C . Tia ME cắt cạnh AD tại điểm N tia CN cắt đường tròn đường kính CM tại điểm I I khác C .a Chứng minh tam giác CBM bằng tam giác CEM và tam giác CEN bằng tam giác CDN , từ đó suy ra CN là tia phân giác của góc ACD.b Chứng minh hệ thức AM2 AN2 BM DN 2.c Chứng minh rằng 3 điểm B, I, D thẳng hàng.d Tính diện tích của tam giác AMN.
Giúp mình giải bài này với ạ.Mình đang cần gấp ạCho tam giác ABC vuông tại A có ah là đường cao. Đường tròn tâm E đường kính BH cắt cạnh AB ở M và đường tròn tâm I đường kính CH cắt cạnh AC ở Na, Chứng minh tứ giác AMHN hình chữ nhậtb, cho biết AB 6 cm AC 8 cm Tính độ dài đoạn thẳng MNc, Chứng minh rằng MN là tiếp tuyến chung của hai đường tròn tâm E và đường tròn tâm I
Đọc tiếp
Giúp mình giải bài này với ạ.Mình đang cần gấp ạ
Cho tam giác ABC vuông tại A có ah là đường cao. Đường tròn tâm E đường kính BH cắt cạnh AB ở M và đường tròn tâm I đường kính CH cắt cạnh AC ở N
a, Chứng minh tứ giác AMHN hình chữ nhật
b, cho biết AB = 6 cm AC = 8 cm Tính độ dài đoạn thẳng MN
c, Chứng minh rằng MN là tiếp tuyến chung của hai đường tròn tâm E và đường tròn tâm I
a:
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
b: \(BC=\sqrt{6^2+8^2}=10\)(cm)
=>AH=6*8/10=4,8(cm)
=>MN=4,8(cm)
c: góc EMN=góc EMH+góc NMH
=góc EHM+góc NAH
=góc HAC+góc HCA=90 độ
=>MN là tiếp tuyến của (E)
góc INM=góc INH+góc MNH
=góc IHN+góc MAH
=góc BAH+góc HBA=90 độ
=>MN là tiếp tuyến của (I)
Đúng 0
Bình luận (0)
Cho hình thang ABCD vuông tại A có cạnh đáy AB bằng 6 cm, cạnh AD bằng 4cm và hai đường chéo vuông góc với nhau. Tính độ dài cạnh DC,CB và đường chéo DB
Cho tam giác ABC vuông tại A ( AC ), đường cao AH. Vẽ hình vuông AHIk (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D
a)Chứng minh rằng AD = AC
b)Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O,H,K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
c)Cho AH = 8. Tính AI
Cho tam giác ABC vuông tại A ( AC ), đường cao AH. Vẽ hình vuông AHIk (điểm H nằm giữa hai điểm C và I), hai đường thẳng KI và AB cắt nhau tại D
a)Chứng minh rằng AD = AC
b)Vẽ hình bình hành ADEC có hai đường chéo cắt nhau tại O, chứng minh rằng ba điểm O,H,K cùng nằm trên đường trung trực của đoạn AI và tứ giác KOEI là hình thang.
c)Cho AH = 8. Tính AI
Cho tam giác ABC vuông tại A có đường cao AH . Đường tròn tâm Ở đường kính BH cắt cạnh AV ở M và đường tròn tâm I đường kính CH cắt cạnh AC ở N A) chứng minh tứ giác AMHN là hình chữ nhật B) cho biết rằng AB =6 , AC =8 . Tính độ dài đoạn MN
a:
Xét đường tròn đường kính HB có
ΔHMB nội tiếp đường tròn
HB là đường kính
Do đó: ΔHMB vuông tại M
Xét đường tròn đường kính HC có
ΔHNC nội tiếp đường tròn
HC là đường kính
Do đó: ΔHNC vuông tại N
Xét tứ giác AMHN có
\(\widehat{NAM}=\widehat{ANH}=\widehat{AMH}=90^0\)
nên AMHN là hình chữ nhật
b: \(BC=\sqrt{6^2+8^2}=10\)
=>AH=6*8/10=4,8
=>MN=4,8
Đúng 0
Bình luận (0)
2/Cho h ình thoi có độ dài hai đường chéo bằng 6cm và 8cm .Tính độ dài cạnh hình thoi?3/Cho hình thang ABCD có AB // CD, AB 4, CD 12.Tính độ dài đường TB của hình thang4/Tam giác ABC vuông tại A, BC 7cm, MB MC, M BC.Tính độ dài AM?5/Cho tam giác ABC có M,N theo thứ tự là trung điểm của AB và AC.Biết MN 4,5 cm.Tính độ dài cạnh BC.6/Cho hình thang ABCD (AB//CD),gọi E,F theo thứ tự là trung điểm của AD và BC.Biết EF 6cm, AB 4cm ,tính độ dài cạnh CD?7/Hình thang có độ dài đáy lớn gấp đôi đáy...
Đọc tiếp
2/Cho h ình thoi có độ dài hai đường chéo bằng 6cm và 8cm .Tính độ dài cạnh hình thoi?
3/Cho hình thang ABCD có AB // CD, AB = 4, CD = 12.Tính độ dài đường TB của hình thang
4/Tam giác ABC vuông tại A, BC = 7cm, MB = MC, M BC.Tính độ dài AM?
5/Cho tam giác ABC có M,N theo thứ tự là trung điểm của AB và AC.Biết MN = 4,5 cm.Tính độ dài cạnh BC.
6/Cho hình thang ABCD (AB//CD),gọi E,F theo thứ tự là trung điểm của AD và BC.Biết EF = 6cm, AB = 4cm ,tính độ dài cạnh CD?
7/Hình thang có độ dài đáy lớn gấp đôi đáy nhỏ . Độ dài đường trung bình là 12 cm. Tính độ dài 2 đáy.
8/Cho hình chữ nhật ABCD, hai đường chéo AC và BD cắt nhau tại O, biết AO = 3cm, Tính độ dài BD?
9/Cho ABC và một điểm O tuỳ ý . Vẽ A/B/C/ đối xứng với ABC qua điểm O .
10/Cho hình vuông ABCD có độ dài đường chéo bằng 10cm.Tính cạnh hình vuông?
11/Cho hình vuông ABCD có độ dài cạnh bằng 3.Tính độ dài đường chéo của hình vuông?
12/T ính độ dài đường trung tuyến ứng với cạnh huyền của một tam giác vuông có các
cạnh góc vuông bằng 3 cm v à 4 cm.
có làm thì mới có ăn
cho hình vuông abcd có 2 đường chéo ac và bd vuông góc với nhau và bằng 12 cm, 2 đường chéo này cắt nhau tại o. từ o ta vẽ 1 hình tròn có đường kính bằng cạnh hình vuông abcd
tính diện tích hình tròn này
Cho hình thang ABCD( AB//CD ), hai đường phân giác của góc C và D cắt nhau tại I thuộc đáy AB. Chứng minh rằng tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang
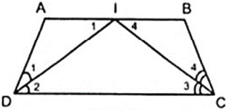
Áp dụng tính chất so le của AB//CD và giả thiết ta có:
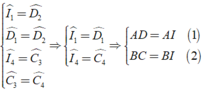
(vì trong một tam giác đối diện với hai góc bằng nhau là hai cạnh bằng nhau)
Cộng vế theo vế của ( 1 ) và ( 2 ) ta được: AD + BC = AB
Điều đó chứng tỏ tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD (AB//CD) có góc A=90°, cạnh BC vuông góc với đường chéo BD, đường phân giác của góc BDC cắt cạnh BC tại I. Cho biết độ dài AB=2,5 cm và góc ABD=60°
a) Chứng minh IDC là tam giác cân
b) Tính độ dài BC, AD, DC và DI















