Cho tam giác ABC không là tam giác vuông. Gọi H và K là chân các đường vuông góc lần lượt hạ từ B và C xuống AC và AB. Chứng minh rằng:
a) Đường tròn đường kính BC đi qua các điểm H và K;
b) KH < BC.
Những câu hỏi liên quan
Cho tam giác ABC có
B
A
C
⏜
60
0
,
A
C
b
,
A
B
c
b
c
. Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc...
Đọc tiếp
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
a) Chứng minh các tứ giác AIEJ, CMJE nội tiếp và E A . E M = E C . E I .
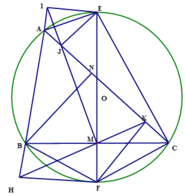
a) Ta có: A I E ^ = A J E ^ = 90 0 nên tứ giác AIEJ nội tiếp.
E M C ^ = E J C ^ = 90 0 nên tứ giác CMJE nội tiếp.
Xét tam giác Δ A E C v à Δ I E M , có
A C E ⏜ = E M I ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác CMJE).
E A C ⏜ = E I M ⏜ ( cùng chắn cung JE của đường tròn ngoại tiếp tứ giác AIEJ).
Do đó hai tam giác Δ A E C ~ Δ I E M đồng dạng
⇒ A E E I = E C E M ⇒ E A . E M = E C . E I (đpcm)
Đúng 0
Bình luận (0)
Cho tam giác ABC có
B
A
C
⏜
60
0
,
A
C
b
,
A
B
c
b
c
. Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc...
Đọc tiếp
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
b) Chứng minh I, J, M thẳng hàng và IJ vuông góc với HK.
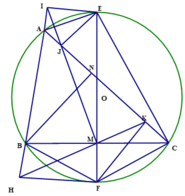
b) Ta có I E M ⏜ = A E C ⏜ ⇒ A E I ⏜ = C E M ⏜ .
Mặt khác A E I ⏜ = A J I ⏜ ( cùng chắn cung IJ), C E M ⏜ = C J M ⏜ ( cùng chắn cung CM). Suy ra C J M ⏜ = A J I ⏜ . Mà I, M nằm hai phía của đường thẳng AC nên C J M ⏜ = A J I ⏜ đối đỉnh suy ra I, J, M thẳng hàng.
Tương tự, ta chứng minh được H, M, K thẳng hàng.
Do tứ giác CFMK nội tiếp nên C F K ⏜ = C M K ⏜ .
Do tứ giác CMJE nội tiếp nên J M E ⏜ = J C E ⏜ .
Mặt khác E C F ⏜ = 90 0 ⇒ C F K ⏜ = J C E ⏜ ( vì cùng phụ với A C F ⏜ ).
Do đó C M K ⏜ = J M E ⏜ ⇒ J M K ⏜ = E M C ⏜ = 90 0 hay I J ⊥ H K
Đúng 0
Bình luận (0)
Cho tam giác ABC có
B
A
C
⏜
60
0
,
A
C
b
,
A
B
c
b
c
. Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc...
Đọc tiếp
Cho tam giác ABC có B A C ⏜ = 60 0 , A C = b , A B = c b > c . Đường kính EF của đường tròn ngoại tiếp tam giác ABC vuông góc với BC tại M (E thuộc cung lớn BC). Gọi I và J là chân đường vuông góc hạ từ E xuống các đường thẳng AB và AC. Gọi H và K là chân đường vuông góc hạ từ F xuống các đường thẳng AB và AC.
c) Tính độ dài cạnh BC và bán kính đường tròn ngoại tiếp tam giác ABC theo b, c.
c)
K ẻ B N ⊥ A C N ∈ A C . B A C ⏜ = 60 0 ⇒ A B N ⏜ = 30 0 ⇒ A N = A B 2 = c 2 ⇒ B N 2 = A B 2 − A N 2 = 3 c 2 4 ⇒ B C 2 = B N 2 + C N 2 = 3 c 2 4 + b − c 2 2 = b 2 + c 2 − b c ⇒ B C = b 2 + c 2 − b c
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC, R là bán kính đường tròn ngoại tiếp tam giác ABC. Xét tam giác đều BCE có R = O E = 2 3 E M = 2 B C 3 3.2 = 1 3 . 3 b 2 + c 2 − b c
Đúng 0
Bình luận (0)
19 tháng 3 2022 lúc 12:10
Cho tam giác ABC vuông tại A, đường cao AH (ABAC). Gọi M và N lần lượt là chân đường vuông góc hạ từ H xuống AB,AC. Gọi K là trung điểm BC. I là giao điểm AK với MNa) Chứng minh: tam giác AHB ∼ tam giác CHAb) Cho AB3, AC4. Tính AHc) Chứng minh: AM.BM+AN.CNBH.CHd) Chứng minh: dfrac{KH}{BH}2left(dfrac{BK}{AB}right)^2-1e) Chứng minh: dfrac{1}{HA}dfrac{1}{HB}+dfrac{1}{HC}
Đọc tiếp
Cho tam giác ABC vuông tại A, đường cao AH (AB<AC). Gọi M và N lần lượt là chân đường vuông góc hạ từ H xuống AB,AC. Gọi K là trung điểm BC. I là giao điểm AK với MN
a) Chứng minh: tam giác AHB ∼ tam giác CHA
b) Cho AB=3, AC=4. Tính AH
c) Chứng minh: AM.BM+AN.CN=BH.CH
d) Chứng minh: \(\dfrac{KH}{BH}=2\left(\dfrac{BK}{AB}\right)^2-1\)
e) Chứng minh: \(\dfrac{1}{HA}=\dfrac{1}{HB}+\dfrac{1}{HC}\)
2 câu d,e mỗi câu 5 coin ạ
Ai lm đc câu nào giúp em với ạ
Đúng 2
Bình luận (0)
Xem thêm câu trả lời
Cho hình vuông ABCD tâm O, điểm M nằm trên đường chéo AC (M khác với A, C). Gọi H, K, P và Q lần lượt là chân đường vuông góc hạ từ M xuống CD, AD, BC và AB.
1) Chứng minh các tứ giác MHCP, MQAK là các hình vuông.
2) Chứng minh rằng tam giác KAB = tam giác HDA và BK vuông gióc với AH.
Giúp mình với ạ. Mình cảm ơn trước
Cho tam giác ABC nhọn nội tiếp đường tròn (O). Gọi H, P, K lần lượt là chân các đường cao hạ từ A, B, C xuống các cạnh BC, AC, AB. Chứng minh OA vuông góc với PK.
Cho tam giác ABC, D là điểm nằm giữa B và C ( AD không vuông góc với BC). Gọi H, K lần lượt là chân các đường vuông góc vẽ từ B, C xuống đường AD. Chứng minh rằng: a) AB + AC > BH + CK; b) BH + CK < BC.
Cho tam giác ABC vuông tại A. M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho AMMD. Gọi I và K lần lượt là chân đường vuông góc hạ từ B và C xuống AD, N là chân đường vuông góc hạ từ M xuống ACa, Chứng minh rằng: BKCI và BK //CIb, Chứng minh KN MCc, Tam giác ABC thỏa mãn thêm điều kiện gì để AIIMMKKD?d, Gọi H là chân đường vuông góc hạ từ D xuống BC. Chứng minh rằng các đường thẳng BI, DH, MN đồng quyGIÚP MÌNH VỚI T_T
Đọc tiếp
Cho tam giác ABC vuông tại A. M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho AM=MD. Gọi I và K lần lượt là chân đường vuông góc hạ từ B và C xuống AD, N là chân đường vuông góc hạ từ M xuống AC
a, Chứng minh rằng: BK=CI và BK //CI
b, Chứng minh KN < MC
c, Tam giác ABC thỏa mãn thêm điều kiện gì để AI=IM=MK=KD?
d, Gọi H là chân đường vuông góc hạ từ D xuống BC. Chứng minh rằng các đường thẳng BI, DH, MN đồng quy
GIÚP MÌNH VỚI T_T
Bạn tham khảo
https://olm.vn/hoi-dap/detail/4685026342.html
Đúng 0
Bình luận (0)
Câu hỏi của Bùi Phương Thảo - Toán lớp 7 - Học toán với OnlineMath
Bạn tham khảo link này nhé!
Đúng 0
Bình luận (0)
tham khảo ở đây nha bạn
link :https://olm.vn/hoi-dap/detail/4685026342.html?pos=2872874683
hok tốt
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho AMMD. Gọi I và K lần lượt là chân đường vuông góc hạ từ B và C xuống AD, N là chân đường vuông góchaj từ M xuống ACa, chứng minh rằng: BKCI và BK song song với CIb, Chứng minh KN MCc, tam giác ABC thỏa mãn thêm điều kiện gì để AIIMMKKDd, Gọi H là chân đường vuông góc hạ từ D xuống BC. Chứng minh rằng các đường thẳng BI, DH,MN đồng quy
Đọc tiếp
Cho tam giác ABC vuông tại A, M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho AM=MD. Gọi I và K lần lượt là chân đường vuông góc hạ từ B và C xuống AD, N là chân đường vuông góchaj từ M xuống AC
a, chứng minh rằng: BK=CI và BK song song với CI
b, Chứng minh KN < MC
c, tam giác ABC thỏa mãn thêm điều kiện gì để AI=IM=MK=KD
d, Gọi H là chân đường vuông góc hạ từ D xuống BC. Chứng minh rằng các đường thẳng BI, DH,MN đồng quy
mik đăng cho Hiếu làm
với lại thầy cho mik nhiều bài toán 7 cx khó nên lên đây ns mấy em làm
đỡ làm chứ
có lợi đôi bên hehehe
Đúng 0
Bình luận (0)
chị ơi chân đường vuông góc là sao cj bọn em chưa hok cái đó
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A, M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho AMMD. Gọi I và K lần lượt là chân đường vuông góc hạ từ B và C xuống AD, N là chân đường vuông góchaj từ M xuống ACa, chứng minh rằng: BKCI và BK song song với CIb, Chứng minh KN MCc, tam giác ABC thỏa mãn thêm điều kiện gì để AIIMMKKDd, Gọi H là chân đường vuông góc hạ từ D xuống BC. Chứng minh rằng các đường thẳng BI, DH,MN đồng quy
Đọc tiếp
Cho tam giác ABC vuông tại A, M là trung điểm của BC, trên tia đối của tia MA lấy điểm D sao cho AM=MD. Gọi I và K lần lượt là chân đường vuông góc hạ từ B và C xuống AD, N là chân đường vuông góchaj từ M xuống AC
a, chứng minh rằng: BK=CI và BK song song với CI
b, Chứng minh KN < MC
c, tam giác ABC thỏa mãn thêm điều kiện gì để AI=IM=MK=KD
d, Gọi H là chân đường vuông góc hạ từ D xuống BC. Chứng minh rằng các đường thẳng BI, DH,MN đồng quy
Câu hỏi của Bùi Phương Thảo - Toán lớp 7 - Học toán với OnlineMath
Bạn tham khảo link này nhé!
Đúng 0
Bình luận (0)