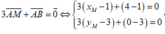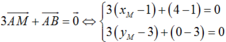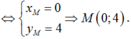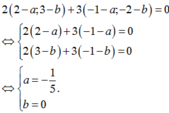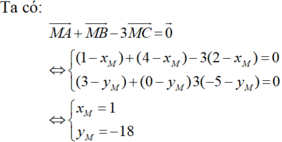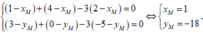Trong mặt phẳng tọa độ Oxy, cho các điểm M (0; 2), N (0; −3) và P(2; −1). Vẽ hình và cho biết trong các điểm đã cho, điểm nào nằm trên, điểm nào nằm trong, điểm nào nằm ngoài đường tròn(O; \(\sqrt{5}\))? Vì sao?

Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ điểm M’ đối xứng với điểm M qua điểm P là:
A. M’(18; 10)
B. M’(18; –10)
C. M'(9/2; 1/2)
D. M’(9; – 7)
Do điểm M’ đối xứng với điểm M qua điểm P nên P là trung điểm MM’.
Suy ra:
x P = x M + x M ' 2 y P = y M + y M ' 2 ⇔ x M ' = 2 x P − x M = 2.9 − 0 = 18 y M ' = 2 y P − y M = 2. ( − 3 ) − 4 = − 10 ⇒ M ' ( 18 ; − 10 )
Đáp án B
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ điểm I của đoạn thẳng MN là:
A. I(0; 3)
B. I(–2; 2)
C. I(-3/2;3)
D. I(–3; 3)
Tọa độ điểm I của đoạn thẳng MN là:
x I = x M + x N 2 = 0 + ( − 3 ) 2 = − 3 2 y I = y M + y N 2 = 4 + 2 2 = 3 ⇒ I − 3 2 ; 3
Đáp án C
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa
3
A
M
→
+
A
B
→
0
→
là A.M( 4; 0) B.M( 0; 4) C.M( 5;3) D.M( 2; 8)
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa 3 A M → + A B → = 0 → là
A.M( 4; 0)
B.M( 0; 4)
C.M( 5;3)
D.M( 2; 8)
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa
3
A
M
→
+
A
B
→
0
→
là A. M(4; 0) B. M(0; 4) C. M(5;3) D. M(2; 8)
Đọc tiếp
Trong mặt phẳng Oxy, cho các điểm A(1;3) và B( 4;0). Tọa độ điểm M thỏa 3 A M → + A B → = 0 → là
A. M(4; 0)
B. M(0; 4)
C. M(5;3)
D. M(2; 8)
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ điểm D sao cho P là trọng tâm tam giác MND là:
A. D(10; 15)
B. D(30; –15)
C. D(20; 10)
D. D(10; 15)
Do P là trọng tâm tam giác MND nên:
x P = x M + x N + x D 3 y P = y M + y N + y D 3 ⇔ x D = 3 x P − x M − x N = 3.9 − 0 − ( − 3 ) = 30 y D = 3 y P − y M − y N = 3. ( − 3 ) − 4 − 2 = − 15 ⇒ D ( 30 ; − 15 )
Đáp án B
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho B(2;3),C(-1;-2) Điểm M thỏa mãn
2
M
B
→
+
3
M
C
→
0
→
Tọa độ điểm M là A. M(1/5;0) B. M(-1/5;0) C. M(0;1/5) D. M(0;-1/5)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho B(2;3),C(-1;-2) Điểm M thỏa mãn 2 M B → + 3 M C → = 0 → Tọa độ điểm M là
A. M(1/5;0)
B. M(-1/5;0)
C. M(0;1/5)
D. M(0;-1/5)
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ trọng tâm G của tam gác MNP là:
A. G(6; 3)
B. G(3;-1/2)
C. G(2; –1)
D. G(2; 1)
Tọa độ trọng tâm G của tam gác MNP là:
x G = x M + x N + x P 3 = 0 + ( − 3 ) + 9 3 = 2 y G = y M + y N + y P 3 = 4 + 2 + ( − 3 ) 3 = 1 ⇒ G ( 2 ; 1 )
Đáp án D
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ; B( 4; 0) ; C(2; -5). Tọa độ điểm M thỏa mãn
M
A
→
+
M
B
→
-
3
M
C
→
0
→
là A. M(1; -18). B. M(1 ;18). C. M(18; -1). D. M(-18; -1).
Đọc tiếp
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ; B( 4; 0) ; C(2; -5). Tọa độ điểm M thỏa mãn M A → + M B → - 3 M C → = 0 → là
A. M(1; -18).
B. M(1 ;18).
C. M(18; -1).
D. M(-18; -1).
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ;; B( 4; 0) ; C( 2; -5). Tọa độ điểm M thỏa mãn
M
A
→
+
M
B
→
-
3
M
C
→
0
→
là A.M( 1; -18) B.M( 1 ;18) C.M( 18; -1 D.M(...
Đọc tiếp
Trong mặt phẳng Oxy , cho các điểm A( 1; 3) ;; B( 4; 0) ; C( 2; -5). Tọa độ điểm M thỏa mãn M A → + M B → - 3 M C → = 0 → là
A.M( 1; -18)
B.M( 1 ;18)
C.M( 18; -1
D.M( -18; -1)