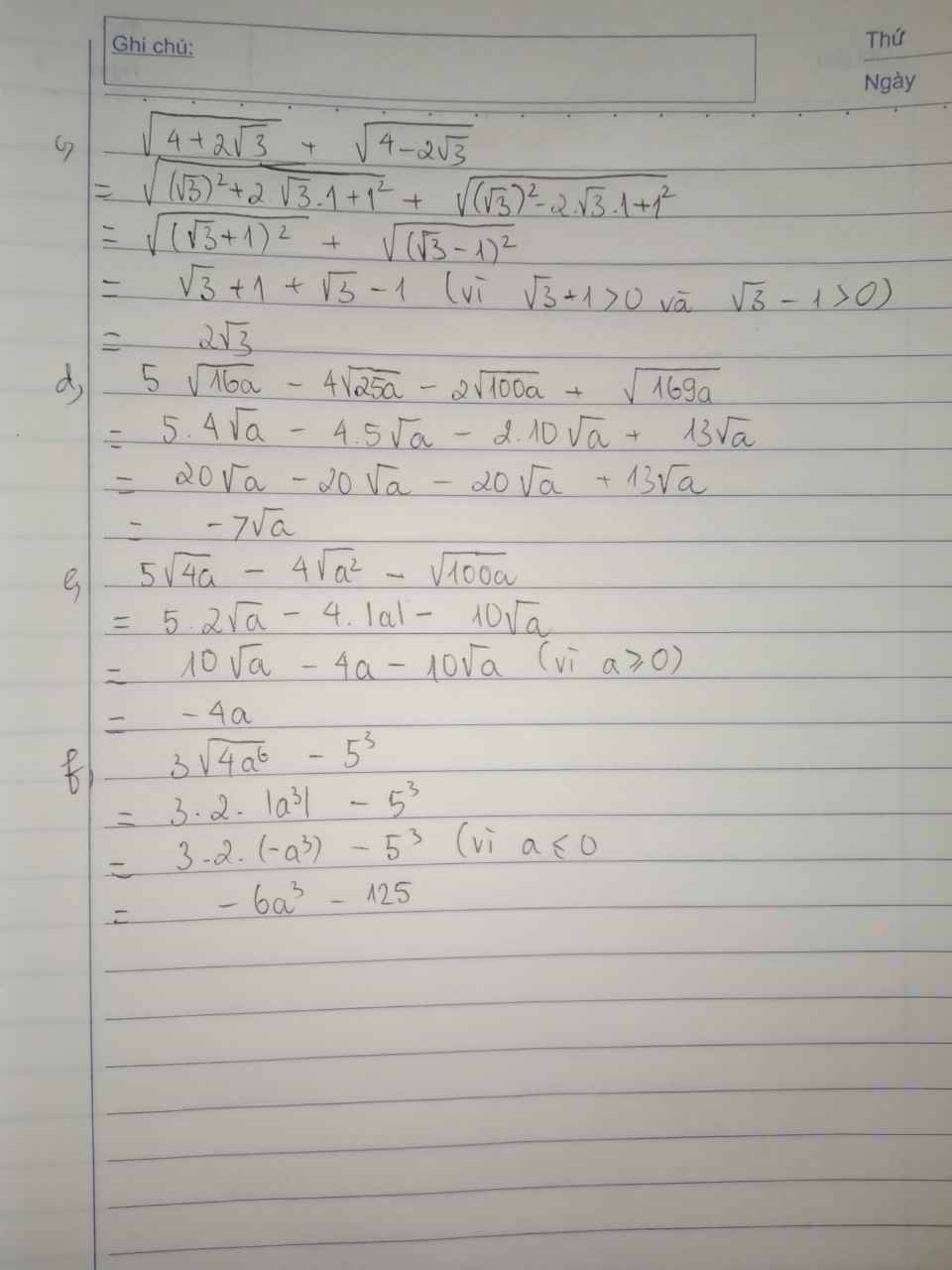a) \(a-\sqrt{a}\)

b) \(-5ab\sqrt{ab}\)

a) Ta có:

\(5\sqrt{a}-4b\sqrt{25a^3}+5a\sqrt{16ab^2}-2\sqrt{9a}\)

\(=5\sqrt{a}-4b.5a\sqrt{a}+5a.4b\sqrt{a}-2.3\sqrt{a}\)

\(=5\sqrt{a}-20ab\sqrt{a}+20ab\sqrt{a}-6\sqrt{a}\) \(=-\sqrt{a}\)

b) Ta có:

\(5a\sqrt{64ab^3}-\sqrt{3}.\sqrt{12a^3b^3}+2ab\sqrt{9ab}\) \(-5b\sqrt{81a^3b}\)

\(=5a.8b\sqrt{ab}-\sqrt{3.12a^3b^3}+2ab.3\sqrt{ab}\) \(-5b.9a\sqrt{ab}\)

\(=40ab\sqrt{ab}-6ab\sqrt{ab}+6ab\sqrt{ab}-45ab\)\(\sqrt{ab}\)

\(=-5ab\sqrt{ab}\)

a)5\(\sqrt{a}\)\(-4b\sqrt{25a^3}+5a\sqrt{16ab^2}-2\sqrt{9a}\)

=5\(\sqrt{a}-20ab\sqrt{a}+20ab\sqrt{a}-6\sqrt{a}\)

= \(\sqrt{a}\left(5-20ab+20ab-6\right)\)

= -\(\sqrt{a}\)

g: \(=\sqrt{5a}-4\sqrt{a}+7\sqrt{a}\)

\(=\sqrt{5a}+3\sqrt{a}\)

b: \(=\dfrac{40}{6+2\sqrt{5}+2\cdot\sqrt{2+2\sqrt{5}}}\)

\(=\dfrac{40}{\left(\sqrt{5}+1\right)^2+\sqrt{2}\cdot\sqrt{4+4\sqrt{5}}}\)

\(=\dfrac{40}{\left(\sqrt{5}+1\right)^2+2\sqrt{2}\cdot\sqrt{\sqrt{5}+1}}\)

\(=\dfrac{40}{\left(\sqrt{\sqrt{5}+1}\right)\left[\left(\sqrt{\sqrt{5}+1}\right)^3+2\sqrt{2}\right]}\)

\(\sqrt{4x^2-4x+1}+2=3x\)

Vì \(VT\ge2\Rightarrow VP\ge2\Rightarrow x\ge\dfrac{2}{3}\)

\(\Rightarrow\sqrt{\left(2x-1\right)^2}+2=3x\Rightarrow\left|2x-1\right|+2=3x\)

\(\Rightarrow2x-1+2=3x\left(x\ge\dfrac{2}{3}\right)\Rightarrow x=1\)

\(7\sqrt{a}-5b\sqrt{16a^3}+4a\sqrt{25ab^2}-3\sqrt{16a}\)

\(=7\sqrt{a}-20ab\sqrt{a}+20ab\sqrt{a}-12\sqrt{a}=-5\sqrt{a}\)

em mới học lớp 5 thôi

em cũng thế mới học lớp 5 thôi

Đáp án : 

 \(5\sqrt{a}-4b\sqrt{25a^3}\) \(+5a\sqrt{16ab^2}\)

= \(5\sqrt{a}-4b\sqrt{\left(5a\right)^2.a}+5a\sqrt{\left(4b\right)^2.a}\)

= \(5\sqrt{a}-\left(-20ab\right)\sqrt{a}+20ab\sqrt{a}\)

= \(5\sqrt{a}\)

a) Ta có: \(\sqrt{125}-4\sqrt{45}+3\sqrt{20}-\sqrt{80}\)

         \(=5\sqrt{5}-4.3\sqrt{5}+3.2\sqrt{5}-4\sqrt{5}\)

         \(=5\sqrt{5}-12\sqrt{5}+6\sqrt{5}-4\sqrt{5}\)

         \(=-5\sqrt{5}\)

         \(\approx-11,18033989\)

b, \(5\sqrt{a}-4b\sqrt{25a^2}+5a\sqrt{16ab^2}-2\sqrt{9a}\)

\(=5\sqrt{a}-20ab+5a.4\sqrt{a}b-6\sqrt{a}\)

\(=-\sqrt{a}-20ab+20a\sqrt{a}b\)

Với x >= 0 ; x khác 16 

\(B=\dfrac{2x+8+x-4\sqrt{x}-8\sqrt{x}-8}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-4\right)}=\dfrac{3x-12\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-4\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+1}\)

2) \(\sqrt{98}-\sqrt{72}+0,5\sqrt{8}\)

\(=7\sqrt{2}-6\sqrt{2}+\sqrt{2}\)

\(=\left(7-6+1\right)\sqrt{2}\)

\(=2\sqrt{2}\)

3) \(\sqrt{9a}-\sqrt{16a}+\sqrt{49a}\)

\(=3\sqrt{a}-4\sqrt{a}+7\sqrt{a}\)

\(=\left(3-4+7\right)\sqrt{a}\)

\(=6\sqrt{a}\)

4) \(\sqrt{16b}+2\sqrt{40b}-3\sqrt{90b}\)

\(=4\sqrt{b}+4\sqrt{10b}-9\sqrt{10b}\)

\(=4\sqrt{b}-5\sqrt{10b}\)

Gấp nha 

a: \(B=\dfrac{x-4\sqrt{x}+4\sqrt{x}+16}{x-4}\cdot\dfrac{\sqrt{x}+2}{x+16}=\dfrac{1}{\sqrt{x}-2}\)

b: Khi x=9 thì B=1/(3-2)=1

Mình sữa đề 1 chút nha

\(5\sqrt{a}-4b\sqrt{25a^3}+5a\sqrt{16ab^2}-2\sqrt{9a}\)

\(=5\sqrt{a}-20ab\sqrt{a}+20ab\sqrt{a}-6\sqrt{a}\)

\(=-\sqrt{a}\)

toi biet nhung ko nho