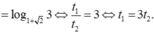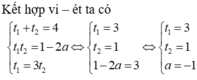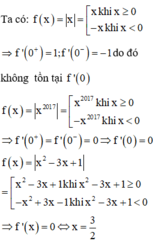phủ định của mệnh đề: "phương trình x2 - 3x + 2 có 2 nghiệm phân biệt"
Những câu hỏi liên quan
Lập mệnh đề phủ định của mỗi mệnh đề sau và nhận xét tính đúng sai của mệnh đề phủ định đó.
a) A: “\(\frac{5}{{1,2}}\) là một phân số”.
b) B: “Phương trình \({x^2} + 3x + 2 = 0\) có nghiệm”.
c) C: “\({2^2} + {2^3} = {2^{2 + 3}}\)”.
d) D: “Số 2 025 chia hết cho 15”.
a) \(\overline A \): “\(\frac{5}{{1,2}}\) không là một phân số”.
Đúng vì \(\frac{5}{{1,2}}\) không là phân số (do 1,2 không là số nguyên)
b) \(\overline B \): “Phương trình \({x^2} + 3x + 2 = 0\) vô nghiệm”.
Sai vì phương trình \({x^2} + 3x + 2 = 0\) có hai nghiệm là \(x = - 1\) và \(x = - 2\).
c) \(\overline C \): “\({2^2} + {2^3} \ne {2^{2 + 3}}\)”.
Đúng vì \({2^2} + {2^3} = 12 \ne 32 = {2^{2 + 3}}\).
d) \(\overline D \): “Số 2 025 không chia hết cho 15”.
Sai vì 2025 = 15. 135, chia hết cho 15.
Đúng 0
Bình luận (0)
Phát biểu mệnh đề phủ định của các mệnh đề sau. Xét tính đúng sai của mỗi mệnh đề và mệnh đề phủ định của nó.
a) Paris là thủ đô của nước Anh
b) 23 là số nguyên tố
c) 2021 chia hết cho 3
d) Phương trình \({x^2} - 3x + 4 = 0\) vô nghiệm.
Mệnh đề phủ định của các mệnh đề trên là:
a) “Paris không phải là thủ đô của nước Anh”
b) “23 không phải là số nguyên tố”
c) “2021 không chia hết cho 3”
d) “Phương trình \({x^2} - 3x + 4 = 0\) có nghiệm”.
+) Xét tính đúng sai:
a) “Paris là thủ đô của nước Anh” là mệnh đề sai.
“Paris không phải là thủ đô của nước Anh” là mệnh đề đúng.
b) “23 là số nguyên tố” là mệnh đề đúng.
“23 không phải là số nguyên tố” là mệnh đề sai.
c) “2021 chia hết cho 3” là mệnh đề sai.
“2021 không chia hết cho 3” là mệnh đề đúng.
d) “Phương trình \({x^2} - 3x + 4 = 0\) vô nghiệm” là mệnh đề đúng.
“Phương trình \({x^2} - 3x + 4 = 0\) có nghiệm” là mệnh đề sai.
Đúng 0
Bình luận (0)
Phát biểu mệnh đề phủ định của mỗi mệnh đề sau và xác định tính đúng sai của mệnh đề phủ định đó.
P: “2 022 chia hết cho 5”
Q: “Bất phương trình 2x + 1 > 0 có nghiệm”.
Mệnh đề phủ định của mệnh đề P là \(\overline P \): “2 022 không chia hết cho 5”
Mệnh đề \(\overline P \) đúng.
Mệnh đề phủ định của mệnh đề Q là \(\overline Q \): “Bất phương trình \(2x + 1 > 0\) vô nghiệm”.
Mệnh đề \(\overline Q \) sai vì bất phương trình \(2x + 1 > 0\) có nghiệm, chẳng hạn: \(x = 0;\;x = 1\).
Đúng 0
Bình luận (0)
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó x =2 là một nghiệm của phương trình x 2 - 4 x - 2 = 0
Mệnh đề sai.
Phủ định là "x = 2 không là nghiệm của phương trình"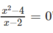 
mệnh đề này đúng.
Đúng 0
Bình luận (0)
Xét tính đúng sai của mỗi mệnh đề sau và phát biểu phủ định của nó. x =2 là một nghiệm của phương trình x 2 - 4 x - 2 = 0
Mệnh đề sai.
Phủ định là "x = 2 không là nghiệm của phương trình"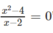 
mệnh đề này đúng.
Đúng 0
Bình luận (0)
Bất phương trình có 2 nghiệm phân biệt
x
1
,
x
2
thỏa mãn
x
1
-
x
2
log
1
+
2
3
Mệnh đề nào dưới đây đúng? A. B. C. D.
Đọc tiếp
Bất phương trình 
có 2 nghiệm phân biệt
x
1
,
x
2
thỏa mãn
x
1
-
x
2
=
log
1
+
2
3
Mệnh đề nào dưới đây đúng?
A. 
B. 
C. 
D. 
Nêu mệnh đề phủ định của mệnh đề sau, cho biết mệnh đề này đúng hay sai?K: “Phương trình
x
4
−
2
x
2
+
2
0
có nghiệm” A.
K
¯
:
“phương trình
x
4
−
2
x
2
+
2...
Đọc tiếp
Nêu mệnh đề phủ định của mệnh đề sau, cho biết mệnh đề này đúng hay sai?
K: “Phương trình x 4 − 2 x 2 + 2 = 0 có nghiệm”
A. K ¯ : “phương trình x 4 − 2 x 2 + 2 = 0 có nghiệm” mệnh đề này sai
B. K ¯ : “phương trình x 4 − 2 x 2 + 2 = 0 vô nghiệm” mệnh đề này sai
C. K ¯ : “phương trình x 4 − 2 x 2 + 2 = 0 vô nghiệm” mệnh đề này đúng
D. K ¯ : “phương trình x 4 − 2 x 2 + 2 = 0 có nghiệm” mệnh đề này đúng
Phương trình
1
+
2
x
+
1
-
2
a
2
-
1
x
-
4
0
có 2 nghiệm phân biệt
x
1
,...
Đọc tiếp
Phương trình
1 + 2 x + 1 - 2 a 2 - 1 x - 4 = 0 có 2 nghiệm phân biệt x 1 , x 2 thỏa mãn x 1 - x 2 = log 1 + 2 3 . Mệnh đề nào dưới đây đúng?
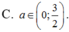
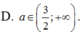
Xét các mệnh đề sau:(1) Nếu hàm số
f
x
x
thì
f
x
0
.(2) Nếu hàm số
f
x
x
2017
thì
f
x
0
.(3) Nếu hàm số
f
x
x
2...
Đọc tiếp
Xét các mệnh đề sau:
(1) Nếu hàm số f x = x thì f ' x = 0 .
(2) Nếu hàm số f x = x 2017 thì f ' x = 0 .
(3) Nếu hàm số f x = x 2 - 3 x + 1 thì phương trình f ' x = 0 có 3 nghiệm phân biệt.
A. (1), (2)
B. (2), (3)
C. (1), (2), (3)
D. (2)
Biết rằng phương trình
log
2
3
x
+
2
π
2
+
log
2
a
2
+
2
x
+
a
2...
Đọc tiếp
Biết rằng phương trình log 2 3 x + 2 π 2 + log 2 a 2 + 2 x + a 2 = 0 có hai nghiệm thực phân biệt x 1 , x 2 . Mệnh đề nào dưới đây đúng
A. x 1 + x 2 2 = 4
B. x 1 x 2 = a 2
C. x 1 - x 2 2 = 4
D. x 1 x 2 = 16 a 2 - 1
Đổi về cơ số tự nhiên, phương trình tương đương với:
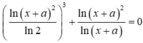
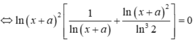
Chọn đáp án C.
Đúng 0
Bình luận (0)