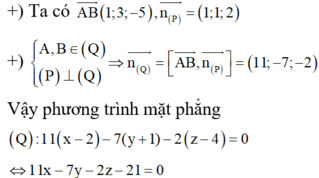Cho hai mặt phẳng (P): x – y – 6 = 0 và (Q). Biết rằng điểm H(2; −1; −2) là hình chiếu vuông góc của gốc tọa độ O(0; 0; 0) xuống mặt phẳng (Q). Tính góc giữa mặt phẳng (P) và mặt phẳng (Q).

Những câu hỏi liên quan
Trong không gian Oxyz, cho hai mặt phẳng
(
P
)
:
x
-
y
-
6
0
và (Q). Biết rằng điểm
H
(
2
;
-
1
;
-
2
)
là hình chiếu vuông góc của gốc tọa độ
O
(
0
;
0
;
0
)
xuống mặt phẳng (Q). Số đo góc giữa mặt phẳng (P) và mặ...
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng ( P ) : x - y - 6 = 0 và (Q). Biết rằng điểm H ( 2 ; - 1 ; - 2 ) là hình chiếu vuông góc của gốc tọa độ O ( 0 ; 0 ; 0 ) xuống mặt phẳng (Q). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng
P
:
x
-
y
-
6
0
và (Q). Biết rằng điểm
H
2
;
-
1
;
-
2
là hình chiếu vuông góc của gốc tọa độ
O
0
;
0
;
0...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai mặt phẳng P : x - y - 6 = 0 và (Q). Biết rằng điểm H 2 ; - 1 ; - 2 là hình chiếu vuông góc của gốc tọa độ O 0 ; 0 ; 0 xuống mặt phẳng (Q). Số đo góc giữa mặt phẳng (P) và mặt phẳng (Q) bằng
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Từ giả thiết, suy ra ![]() là một VTPT của mặt phẳng (Q)
là một VTPT của mặt phẳng (Q)
Mặt phẳng (P) có VTPT ![]()
Gọi φ là góc giữa hai mặt phẳng (P) và (Q). Ta có
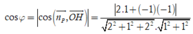
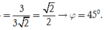
Chọn B.
Đúng 0
Bình luận (0)
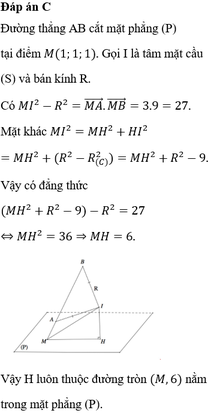
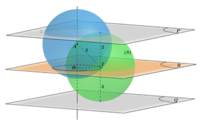
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x-y-2z-20 và mặt phẳng (Q): 2x-y-2z+100 song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó A.
r
4
2...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho mặt phẳng (P): 2x-y-2z-2=0 và mặt phẳng (Q): 2x-y-2z+10=0 song song với nhau. Biết A(1;2;1) là điểm nằm giữa hai mặt phẳng (P) và (Q). Gọi (S) là mặt cầu qua A và tiếp xúc với cả hai mặt phẳng (P) và (Q). Biết rằng khi (S) thay đổi thì tâm của nó luôn nằm trên một đường tròn. Tính bán kính r của đường tròn đó
A. r = 4 2 3
B. r = 2 2 3
C. r = 5 3
D. r = 2 5 3
Chọn A
Điểm M(1;0;0) là 1 điểm thuộc (P)
Vì (P) // (Q) nên
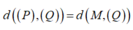
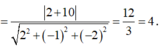
Giả sử I(a;b;c) là tâm của (S). Vì (S) tiếp xúc với cả (P) và (Q) nên bán kính mặt cầu (S) là:
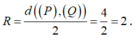
Do đó IA = 2 nên I luôn thuộc mặt cầu (T) tâm A, bán kính 2.
Ngoài ra
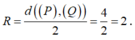
![]()
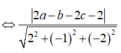
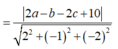
![]()
![]()
![]()
Do đó I luôn thuộc mặt phẳng (R): 2x-y-2z+4=0.
Gọi H là hình chiếu vuông góc của A lên (R). Vì A, (R) cố định nên H cố định.
Ta có
![]()
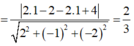
![]()
do đó tam giác AHI vuông tại H nên
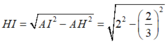
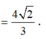
Vậy I luôn thuộc đường tròn tâm H, nằm trên mặt phẳng (R), bán kính
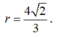
Đúng 0
Bình luận (0)
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-1;-1),B(4;-5;-5) và mặt phẳng (P):x+y+z-30. Mặt cầu (S) thay đổi qua hai điểm A,B và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có tâm H và bán kính bằng 3. Biết rằng H luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó. A.
21
. B.
2
6
. C. 6. D.
3
3
.
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, cho hai điểm A(2;-1;-1),B(4;-5;-5) và mặt phẳng (P):x+y+z-3=0. Mặt cầu (S) thay đổi qua hai điểm A,B và cắt mặt phẳng (P) theo giao tuyến là đường tròn (C) có tâm H và bán kính bằng 3. Biết rằng H luôn thuộc một đường tròn cố định. Tìm bán kính của đường tròn đó.
A. 21 .
B. 2 6 .
C. 6.
D. 3 3 .
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 0, (Q): 2x - y - 2z + 1 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu? A. 4π B. π C. 2π D. 16π
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P): 2x - y - 2z + 7 = 0, (Q): 2x - y - 2z + 1 = 0. Biết rằng mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q). Hỏi diện tích của mặt cầu (S) là bao nhiêu?
A. 4π
B. π
C. 2π
D. 16π
Đáp án A
Hai mặt phẳng (P) và (Q) có cùng vecto pháp tuyến là: n → (2; -1; -2)
Điểm A(-3; 1; 0) thuộc mặt phẳng (P) nhưng không thuộc mặt phẳng (Q).
Do đó, hai mặt phẳng (P) và (Q) song song với nhau.
Khoảng cách giữa hai mặt phẳng là:
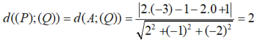
Vì mặt cầu (S) tiếp xúc với cả hai mặt phẳng (P) và (Q) nên khoảng cách giữa hai mặt phẳng (P) và (Q) chính là đường kính của mặt cầu: 2R = 2 nên R = 1.
Diện tích của mặt cầu (S) là: S = 4π R 2 = 4 π
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho hai điểm
A
(
2
;
-
1
;
4
)
,
B
(
3
;
2
;
-
1
)
và mặt phẳng (P):
x
+
y
+
2
z
-
4
0
. Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phuơng trình là A.
11
x...
Đọc tiếp
Trong không gian Oxyz, cho hai điểm A ( 2 ; - 1 ; 4 ) , B ( 3 ; 2 ; - 1 ) và mặt phẳng (P): x + y + 2 z - 4 = 0 . Mặt phẳng (Q) đi qua hai điểm A, B và vuông góc với mặt phẳng (P) có phuơng trình là
A. 11 x − 7 y − 2 z + 21 = 0
B. 11 x + 7 y - 2 z - 7 = 0
C. 11 x - 7 y - 2 z - 21 = 0
D. 11 x + 7 y - 2 z + 7 = 0
Trong không gian Oxyz, cho điểm A(1;1;-2) và hai mặt phẳng (P): 3x - y +1 0, (Q): x - 2z - 3 0. Phương trình đường thẳng d qua điểm A đồng thời song song với cả hai mặt phẳng (P), (Q) là A.
x
2
+
t
y
−...
Đọc tiếp
Trong không gian Oxyz, cho điểm A(1;1;-2) và hai mặt phẳng (P): 3x - y +1 = 0, (Q): x - 2z - 3 = 0. Phương trình đường thẳng d qua điểm A đồng thời song song với cả hai mặt phẳng (P), (Q) là
A. x = 2 + t y = − 6 + t z = 1 − 2 t .
B. x = 5 + 2 t y = 13 + 6 t z = t .
C. x = 1 + 2 t y = 1 − 6 t z = − 2 + t .
D. x = 2 + t y = 6 + t z = 1 − 2 t .
Đáp án B
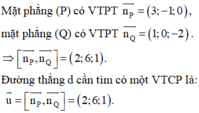
Vì A 1 ; 1 ; − 2 ∈ d nên phương trình của đường thẳng d là: x = 1 + 2 t y = 1 + 6 t z = − 2 + t
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho 2 điểm A(1;0;1) và B(-1;1;0), mặt phẳng (P):\(x+y-2z-5=0\) và mặt cầu \(\left(S\right):x^2+y^2+z^2-2x+2y-6=0\).
Viết phương trình mặt phẳng (Q), biết (Q) vuông góc với (P), song song với đường thẳng AB và tiếp xúc với mặt cầu (S)
Mặt phẳng (P) có vec tơ pháp tuyến \(\overrightarrow{n}=\left(1;1;-2\right);\overrightarrow{AB}=\left(-2;1;-1\right)\)
Ta có \(\left[\overrightarrow{n};\overrightarrow{AB}\right]=\left(1;5;3\right)\)
(Q) vuông góc với (P), song song với đường thẳng AB suy ra (Q) có vectơ pháp tuyến là \(\left[\overrightarrow{n_1};\overrightarrow{AB}\right]=\left(1;5;3\right)\) nên phương trình mặt phẳng (Q) có dạng \(x+5y+3z+m=0\)
Mặt cầu (S) có tâm \(I\left(1;-1;1\right)\), bán kính R = 3
Mặt phẳng (Q) tiếp xúc với (S) có \(d\left(I,\left(Q\right)\right)=R\Leftrightarrow\frac{\left|1-5+3+m\right|}{\sqrt{35}}\)
\(\Leftrightarrow\left|m-1\right|=3\sqrt{35}\Leftrightarrow\begin{cases}m=1+3\sqrt{35}\\m=1-3\sqrt{35}\end{cases}\)
- Với \(m=1+3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1+3\sqrt{35}=0\)
- Với \(m=1-3\sqrt{35}\) ta có phương trình mặt phẳng (Q) là : \(x+5y+3z+1-3\sqrt{35}=0\)
Đúng 0
Bình luận (0)
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng
P
: x+y-z-20,
Q
: x-y+z-10
Đọc tiếp
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng P : x+y-z-2=0, Q : x-y+z-1=0
![]()
![]()
![]()
![]()
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng
(
P
)
:
x
+
y
-
z
-
2
0
,
(
Q
)
:
x
-
y
+
z
-
1
...
Đọc tiếp
Phương trình mặt phẳng đi qua điểm A(1;1;1) và vuông góc với hai mặt phẳng ( P ) : x + y - z - 2 = 0 , ( Q ) : x - y + z - 1 = 0 là
A. x + y + z - 3 = 0
B. x - 2y + z = 0
C. x + z - 2 = 0
D. x + y - 2 = 0