Trong không gian Oxyz, cho mặt phẳng (α) đi qua ba điểm A(0; 1; 1), B(2; 4; 3), C(5; 3; 1).
a) Tìm tọa độ một cặp vectơ chỉ phương của mặt phẳng (α).
b) Tìm tọa độ một vectơ pháp tuyến của mặt phẳng (α).
c) Lập phương trình của mặt phẳng (α).
Những câu hỏi liên quan
Trong không gian Oxyz, cho ba điểm M(1;2;4); N(0;1;2); P(2;1;3) và mặt phẳng
α
: x+Ay+Bx+C0 . Biết
α
song song với OP và đi qua hai điểm M, N. Giá trị của biểu thức A+B-C là A. 1. B. -1. C. -5. D. 0.
Đọc tiếp
Trong không gian Oxyz, cho ba điểm M(1;2;4); N(0;1;2); P(2;1;3) và mặt phẳng α : x+Ay+Bx+C=0 . Biết α song song với OP và đi qua hai điểm M, N. Giá trị của biểu thức A+B-C là
A. 1.
B. -1.
C. -5.
D. 0.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng
α
:
x
−
4
y
+
z
0
. Viết phương trình mặt phẳng
β
đi qua A và song song với mặt phẳng
α
. A.
x
−
4
y
+
z
−
4
0
B.
x
−
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và mặt phẳng α : x − 4 y + z = 0 . Viết phương trình mặt phẳng β đi qua A và song song với mặt phẳng α .
A. x − 4 y + z − 4 = 0
B. x − 4 y + z + 4 = 0
C. 2 x + y + 2 z − 10 = 0
D. 2 x + y + 2 z + 10 = 0
Trong không gian với hệ tọa độ Oxyz, cho điểm
A
1
;
2
;
3
và mặt phẳng
α
:
x
−
4
y
+
z
0
. Viết phương trình mặt phẳng
β
đi qua A và song song với mặt phẳng
α
. A.
x
−
4
y
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A 1 ; 2 ; 3 và mặt phẳng α : x − 4 y + z = 0 . Viết phương trình mặt phẳng β đi qua A và song song với mặt phẳng α .
A. x − 4 y + z − 4 = 0
B. x − 4 y + z + 4 = 0
C. 2 x + y + 2 z − 10 = 0
D. 2 x + y + 2 z + 10 = 0
Đáp án B.
Vì β song song với α nên loại đáp án C và D.
Thử trực tiếp thấy điểm A 1 ; 2 ; 3 thuộc mặt phẳng x − 4 y + z + 4 = 0 .
Do đó đáp án đúng là B.
Đúng 0
Bình luận (0)
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
α
:
2
x
-
y
-
3
z
+
10
0
và điểm
M
2
;
-
2
;
3
. Mặt phẳng
P
đi qua
M
và song s...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng α : 2 x - y - 3 z + 10 = 0 và điểm M 2 ; - 2 ; 3 . Mặt phẳng P đi qua M và song song với mặt phẳng α có phương trình là:
A. P : 2 x - y - 3 z + 3 = 0
B. P : 2 x - y - 3 z - 3 = 0
C. P : 2 x - 2 y - 3 z + 3 = 0
D. P : 2 x - 2 y + 3 z - 15 = 0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm
A
1
;
0
;
1
;
B
2
;
1
;
2
và mặt phẳng
P
:
x
+
2
y
+
3
z
+
3
0
. Phương trình mặt...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A 1 ; 0 ; 1 ; B 2 ; 1 ; 2 và mặt phẳng P : x + 2 y + 3 z + 3 = 0 . Phương trình mặt phẳng α đi qua hai điểm A, B và vuông góc với mặt phẳng (P) là:
A. x + 2y - z + 6 = 0
B. x + 2y - 3z + 6 = 0
C. x - 2y + z - 2 = 0
D. x + 2y - 3z + 6 = 0
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
α
:
2
x
-
y
-
3
z
+
10
0
và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng
α
có phương trình là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng α : 2 x - y - 3 z + 10 = 0 và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng α có phương trình là:
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;0;1), B(2;1;2) và mặt phẳng (P):x+2y+3z+30. Phương trình mặt phẳng
(
α
)
đi qua hai điểm A, B và vuông góc với mặt phẳng là: A. x + 2y -z +6 0 B.x + 2y -3z +6 0 C. x -2y + z-2 0 D. x + 2y -3z +6 0
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(1;0;1), B(2;1;2) và mặt phẳng (P):x+2y+3z+3=0. Phương trình mặt phẳng ( α ) đi qua hai điểm A, B và vuông góc với mặt phẳng là:
A. x + 2y -z +6 =0
B.x + 2y -3z +6 =0
C. x -2y + z-2 =0
D. x + 2y -3z +6 =0
Trong không gian với hệ toạ độ Oxyz, (α) là mặt phẳng đi qua điểm
A
(
2
;
-
1
;
5
)
và vuông góc với hai mặt phẳng
(
P
)
:
3
x
–
2
y
+
z
–
1
0
v
à
(...
Đọc tiếp
Trong không gian với hệ toạ độ Oxyz, (α) là mặt phẳng đi qua điểm A ( 2 ; - 1 ; 5 ) và vuông góc với hai mặt phẳng ( P ) : 3 x – 2 y + z – 1 = 0 v à ( Q ) : 5 x – 4 y + 3 z + 10 = 0 . Phương trình mặt phẳng (α) là:
A. x + 2y + z- 5 = 0.
B. 2x – 4y – 2z – 9 = 0.
C. x - 2y + z -1 = 0
D. x- 2y- z + 1 = 0
Chọn A.
Mặt phẳng (α) vuông góc với 2 mặt phẳng (P) và (Q) nên có một VTPT là
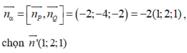
Phương trình mặt phẳng (α) là:
1(x - 2) + 2(y + 1) + 1.(z - 5) = 0 hay x + 2y + z – 5 = 0
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho mặt phẳng
(
α
)
: 2x + 3y - 2z + 12 0. Gọi A, B, C lần lượt là giao điểm của
(
α
)
với ba trục tọa độ, đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với
(
α
)
có phương trình là A.
x
-
3
2
y
-
2
3...
Đọc tiếp
Trong không gian Oxyz, cho mặt phẳng ( α ) : 2x + 3y - 2z + 12= 0. Gọi A, B, C lần lượt là giao điểm của ( α ) với ba trục tọa độ, đường thẳng đi qua tâm đường tròn ngoại tiếp tam giác ABC và vuông góc với ( α ) có phương trình là
A. x - 3 2 = y - 2 3 = z - 3 - 2
B. x + 3 2 = y - 2 - 3 = z - 3 2
C. x + 3 2 = y + 2 3 = z - 3 - 2
D. x - 3 2 = y - 2 3 = z + 3 - 2
Trong không gian với hệ tọa độ Oxyz, phương trình
(
α
)
mặt phẳng
A
(
0
;
−
1
;
0
)
,
B
(
2
;
0
;
0
)
;
C
(
0
;
0
;
3
)
đi qua điểm là A.
x
2
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, phương trình ( α ) mặt phẳng A ( 0 ; − 1 ; 0 ) , B ( 2 ; 0 ; 0 ) ; C ( 0 ; 0 ; 3 ) đi qua điểm là
A. x 2 + y 1 + z 3 = 1.
B. x 2 + y − 1 + z 3 = 0.
C. x − 1 + y 2 + z 3 = 1.
D. x 2 + y − 1 + z 3 = 1.