Các câu hỏi tương tự
Trong không gian với hệ tọa độ Oxyz cho điểm M (3;-1;-2) và mặt phẳng (
α
): 3x-y+2z+40. Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với (
α
)? A. 3x+y-2z-140 B. 3x-y+2z+60 C. 3x-y+2z-60 D. 3x-y-2z+60
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho điểm M (3;-1;-2) và mặt phẳng ( α ): 3x-y+2z+4=0. Phương trình nào dưới đây là phương trình mặt phẳng đi qua M và song song với ( α )?
A. 3x+y-2z-14=0
B. 3x-y+2z+6=0
C. 3x-y+2z-6=0
D. 3x-y-2z+6=0
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;-1;5), B(1;-2;3). Mặt phẳng
α
đi qua hai điểm A,B và song song với trục Ox có vect ơ pháp tuyến
n
→
(
0
;
a
;
b
)
. Khi đó , tỷ số
a
b
bằng A. 2 B. -2 C.
-
3
2
D.
3...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(2;-1;5), B(1;-2;3). Mặt phẳng α đi qua hai điểm A,B và song song với trục Ox có vect ơ pháp tuyến n → ( 0 ; a ; b ) . Khi đó , tỷ số a b bằng
A. 2
B. -2
C. - 3 2
D. 3 2
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng
α
:
2
x
-
y
-
3
z
+
10
0
và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng
α
có phương trình là:
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng α : 2 x - y - 3 z + 10 = 0 và điểm M(2;-2;3). Mặt phẳng (P) đi qua M và song song với mặt phẳng α có phương trình là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng
d
:
x
-
3
1
y
-
3
3
z
2
, mặt phẳng (α): x+y-z+30 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d : x - 3 1 = y - 3 3 = z 2 , mặt phẳng (α): x+y-z+3=0 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).
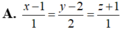
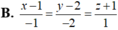
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng
d
:
x
-
3
1
y
-
3
3
z
2
, mặt phẳng (α): x+y-z+30 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz cho đường thẳng d : x - 3 1 = y - 3 3 = z 2 , mặt phẳng (α): x+y-z+3=0 và điểm A (1;2;-1). Viết phương trình đường thẳng Δ đi qua A cắt d và song song với mặt phẳng (α).
![]()
![]()
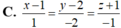
![]()
Trong không gian Oxyz cho ba điểm A (0;2;-2), B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc mặt phẳng (
α
): 2x -y +2z + 7 0 sao cho biểu thức
3
M
A
→
+
5
M
C
→
-
7
M
C...
Đọc tiếp
Trong không gian Oxyz cho ba điểm A (0;2;-2),
B (-3;1;-1), C (3;-1;2). Điểm M (a;b;c) thuộc
mặt phẳng ( α ): 2x -y +2z + 7 = 0 sao cho biểu
thức 3 M A → + 5 M C → - 7 M C → đạt giá trị nhỏ nhất.
Tính a+b+c
![]()
![]()
![]()
![]()
Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto làm vectơ chỉ phương và song song với mặt phẳng (P): 2x+y+z0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng: A. 15 B. 13 C. 16 D. 14
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho các điểm M (2;2; -3) và N (-4; 2; 1). Gọi Δ là đường thẳng đi qua M, nhận vecto làm vectơ chỉ phương và song song với mặt phẳng (P): 2x+y+z=0 sao cho khoảng cách từ N đến Δ đạt giá trị nhỏ nhất. Biết |a|, |b| là hai số nguyên tố cùng nhau. Khi đó |a| + |b| + |c| bằng:
A. 15
B. 13
C. 16
D. 14
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-40 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục xOx là:
A
.
M
-
1
2
;
0
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm A(0;1;2), mặt phẳng (α): x-y+z-4=0 và mặt cầu (S): (x-3)²+ (y-1)²+ (z-2)²=16. Gọi (P) là mặt phẳng đi qua A, vuông góc với (α) và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
A . M - 1 2 ; 0 ; 0
B . M - 1 3 ; 0 ; 0
C . M 1 ; 0 ; 0
D . M 1 3 ; 0 ; 0
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng:
α
:
3
x
+
(
m
-
1
)
y
+
4
z
-
2
0
,
β
:
n
x
+
(
m
+
2
)
y
+
2
z
+
4
0
,
Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β). A.
m...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng:
α : 3 x + ( m - 1 ) y + 4 z - 2 = 0 , β : n x + ( m + 2 ) y + 2 z + 4 = 0 ,
Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β).
A. m = - 3 , n = 1 2
B. m = 5 , n = 2 3
C. m = - 5 , n = 3 2
D. m = 5 , n = - 3 2




