Tìm cực trị của các hàm số sau:
a) y = 2x3 + 3x2 – 36x + 1; b) \(\dfrac{x^2-8x+10}{x-2}\); c) \(y=\sqrt{-x^2+4}\).
Những câu hỏi liên quan
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau: y = 2 x 3 + 3 x 2 - 3
TXĐ: D = R
y' = 6x2 + 6x - 36
y' = 0 ⇔ x = -3 hoặc x = 2
Bảng biến thiên:
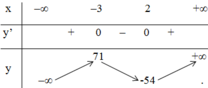
Kết luận :
Hàm số đạt cực đại tại x = -3 ; yCĐ = 71
Hàm số đạt cực tiểu tại x = 2; yCT = -54.
Đúng 0
Bình luận (0)
Tìm cực trị của hàm số
y
2
x
3
+
3
x
2
+
4
. A.
x
C
Đ
-1,
x
C
T
0 B.
y
C
Đ
5,
y...
Đọc tiếp
Tìm cực trị của hàm số y = 2 x 3 + 3 x 2 + 4 .
A. x C Đ = -1, x C T = 0
B. y C Đ = 5, y C T = 4
C. x C Đ = 0, x C T = - 1
D. y C Đ = 4, y C T = 5
Tìm cực trị của hàm số y 2x3 + 3x2 + 4? A. xCĐ -1, xCT 0 B. yCĐ 5, yCT 4 C. xCĐ 0, xCT - 1 D. yCĐ 4, yCT 5
Đọc tiếp
Tìm cực trị của hàm số y= 2x3 + 3x2 + 4?
A. xCĐ = -1, xCT = 0
B. yCĐ = 5, yCT = 4
C. xCĐ = 0, xCT = - 1
D. yCĐ = 4, yCT = 5
Tìm tổng giá trị cực đại và giá trị cực tiểu của hàm số y = - 2 x 3 + 3 x 2 + 18
A.38
B.37
C.40
D.39
Tìm các số thực m để hàm số
y
m
+
2
x
3
+
3
x
2
+
m
x
-
5
có cực trị. A.
m
≠
-
2
hoặc -3m1 B. -3m1 C. m-3 hoặc m1 D. -2m1
Đọc tiếp
Tìm các số thực m để hàm số y = m + 2 x 3 + 3 x 2 + m x - 5 có cực trị.
A. m ≠ - 2 hoặc -3<m<1
B. -3<m<1
C. m<-3 hoặc m>1
D. -2<m<1
Cho hàm số
y
m
+
2
x
3
+
3
x
2
+
m
x
−
5
. Tìm tất cả các giá trị của tham số thực m để điểm cực đại, cực tiểu của hàm số đã cho có hoành độ là một số dương. A. -3 m -2 B. -3 m 1 C. m -2 D. m 0
Đọc tiếp
Cho hàm số y = m + 2 x 3 + 3 x 2 + m x − 5 . Tìm tất cả các giá trị của tham số thực m để điểm cực đại, cực tiểu của hàm số đã cho có hoành độ là một số dương.
A. -3 < m < -2
B. -3 < m < 1
C. m < -2
D. m < 0
Đáp án A.
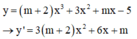
Hàm số đã cho có điểm cực đại và điểm cực tiểu đều có hoành độ dương
Đúng 0
Bình luận (0)
Gọi x = a và x = b là các điểm cực trị của hàm số y = 2x3 – 3x2 – 18x - 1. Khi đó A = a + b – 2ab bằng:
A. -7
B. 5
C. 7
D. -5
Hàm số y 3x2 – 2x3 đạt cực trị tại A. xCĐ 0; xCT -1 B. xCĐ 1; xCT 0 C. xCĐ 0; xCT 1 D. xCĐ -1; xCT 0
Đọc tiếp
Hàm số y = 3x2 – 2x3 đạt cực trị tại
A. xCĐ = 0; xCT = -1
B. xCĐ = 1; xCT = 0
C. xCĐ = 0; xCT = 1
D. xCĐ = -1; xCT = 0
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = - 2 x 3 + 3 x 2 + 1
A. y = x+1
B. y = -x+1
C. y = x-1
D. y = -x-1
Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = - 2 x 3 + 3 x 2 + 1
A. y=x+1
B. y=-x+1
C. y=x-1
D. y=-x-1
