TXĐ: D = R
y' = 6x2 + 6x - 36
y' = 0 ⇔ x = -3 hoặc x = 2
Bảng biến thiên:
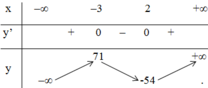
Kết luận :
Hàm số đạt cực đại tại x = -3 ; yCĐ = 71
Hàm số đạt cực tiểu tại x = 2; yCT = -54.
TXĐ: D = R
y' = 6x2 + 6x - 36
y' = 0 ⇔ x = -3 hoặc x = 2
Bảng biến thiên:

Kết luận :
Hàm số đạt cực đại tại x = -3 ; yCĐ = 71
Hàm số đạt cực tiểu tại x = 2; yCT = -54.
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = sin2x – x
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
y = x 4 + 2 x 2 - 3
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
y = x + 1 x
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm s f(x) = x(x^2 – 3).
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = x 4 - 2 x 2 + 1
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = x 5 - x 3 - 2 x + 1
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = sinx + cosx
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
y = x 3 1 - x 2
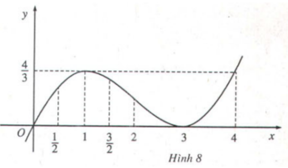
Sử dụng đồ thị, hãy xem xét các hàm số sau đây có cực trị hay không.
• y = -2x + 1;
• y = x/3(x-3)2 (H.8).