TXĐ: D = R
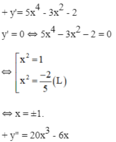
y"(-1) = -20 + 6 = -14 < 0
⇒ x = -1 là điểm cực đại của hàm số.
y"(1) = 20 – 6 = 14 > 0
⇒ x = 1 là điểm cực tiểu của hàm số.
TXĐ: D = R
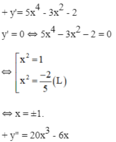
y"(-1) = -20 + 6 = -14 < 0
⇒ x = -1 là điểm cực đại của hàm số.
y"(1) = 20 – 6 = 14 > 0
⇒ x = 1 là điểm cực tiểu của hàm số.
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = sin2x – x
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
y = x + 1 x
Áp dụng quy tắc I, hãy tìm các điểm cực trị của hàm s f(x) = x(x^2 – 3).
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = x 4 - 2 x 2 + 1
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
y = x 4 + 2 x 2 - 3
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau: y = 2 x 3 + 3 x 2 - 3
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = sinx + cosx
Áp dụng Quy tắc 1, hãy tìm các điểm cực trị của các hàm số sau:
y = x 3 1 - x 2
sử dụng nguyên tắc 2 tìm cực trị của hàm số F(x)=x+1/x