Tính độ hụt khối của hai hạt nhân bất kì được cho trong Bảng 15.1.
Cho một phản ứng hạt nhân tỏa năng lượng. Gọi Δ m t r là tổng độ hụt khối lượng các hạt nhân trước phản ứng; Δ m s là tổng độ hụt khối lượng các hạt nhân sau phản ứng. c là tốc độ ánh sáng trong chân không. Năng lượng tỏa ra của phản ứng là Q(Q>0) được tính bằng biểu thức
A. Q = Δ m t r − Δ m s c 2
B. Δ m t r − Δ m s c
C. Q = Δ m s − Δ m t r c 2
D. Q = Δ m s − Δ m t r c
Đáp án C
Năng lượng phản ứng tỏa ra được tính bằng: Q = Δ m s − Δ m t r c 2
Cho một phản ứng hạt nhân tỏa năng lượng. Gọi Δ m t r là tổng độ hụt khối lượng các hạt nhân trước phản ứng; Δ m s là tổng độ hụt khối lượng các hạt nhân sau phản ứng. c là tốc độ ánh sáng trong chân không. Năng lượng tỏa ra của phản ứng là Q (Q>0) được tính bằng biểu thức
A. Q = Δ m t r − Δ m s c 2
B. Δ m t r − Δ m s c
C. Q = Δ m s − Δ m t r c 2
D. Q = Δ m s − Δ m t r c
Đáp án C
Năng lượng phản ứng tỏa ra được tính bằng: Q = Δ m s − Δ m t r c 2
Ta dùng prôtôn có 2,0MeV vào hạt nhân 7Li đứng yên thì thu hai nhân X có cùng động năng. Năng lượng liên kết của hạt nhân X là 28,3MeV và độ hụt khối của hạt 7Li là 0,0421u. Cho 1u = 931,5MeV/c2; khối lượng hạt nhân tính theo u xấp xỉ bằng số khối. Tốc độ của hạt nhân X bằng:
A. 1,96m/s.
B. 2,20m/s.
C. 2,16.107m/s.
D. 1,93.107m/s.
Đáp án C:
Ta có phương trình phản ứng: ![]()
Năng lượng liên kết của hạt 7Li là: ∆ ELi = ∆ mLi . c2 = 0,0421.931,5 = 39,216 MeV
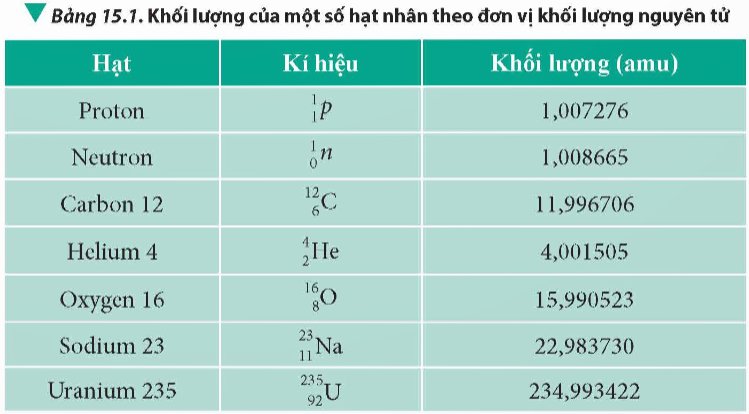
∆ E = 2 ∆ EX - ∆ ELi - ∆ Ep = 2.28,3 - 39,216 – 0 = 17,385MeV
∆ E = 2KX - Kp → KX = ( ∆ E + Kp)/2 = 9,692MeV
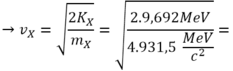
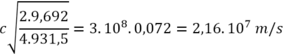
Ta dùng prôtôn có 2,0MeV vào nhân Li 7 đứng yên thì thu hai nhân X có cùng động năng. Năng lượng liên kết của hạt nhân X là 28,3MeV và độ hụt khối của hạt Li 7 là 0,042lu. Cho 1 u = 931 , 5 MeV / c 2 ; khối lượng hạt nhân tính theo u xấp xỉ bằng số khối. Tốc độ của hạt nhân X bằng
A. l,96m/s.
B. 2,20m/s
C. 2 , 16 . 10 7 m/s.
D. 1 , 93 . 10 7 m/s
Kí hiệu ∆ m là độ hụt khối của mỗi hạt nhân tham gia phản ứng hạt nhân A + B → C + D . Năng lượng E tỏa ra trong phản ứng được tính bằng biểu thức:
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Hai hạt nhân X và Y có độ hụt khối bằng nhau và số nuclôn của hạt nhân X nhỏ hơn số nuclôn của hạt nhân Y thì
A. năng lượng liên kết riêng của hai hạt nhân bằng nhau
B. hạt nhân X bền vững hơn hạt nhân Y
C. năng lượng liên kết của hạt nhân X lớn hơn năng lượng liên kết của hạt nhân Y
D. hạt nhân Y bền vững hơn hạt nhân X
Đáp án B
Độ hụt khối bằng nhau → Wlk bằng nhau → Wlkr của X lớn hơn Y → X bền hơn Y.
Hai hạt nhân X và Y có độ hụt khối bằng nhau và số nuclôn của hạt nhân X nhỏ hơn số nuclôn của hạt nhân Y thì
A. năng lượng liên kết riêng của hai hạt nhân bằng nhau
B. hạt nhân X bền vững hơn hạt nhân Y
C. năng lượng liên kết của hạt nhân X lớn hơn năng lượng liên kết của hạt nhân Y
D. hạt nhân Y bền vững hơn hạt nhân X
Đáp án B
Độ hụt khối bằng nhau → Wlk bằng nhau → Wlkr của X lớn hơn Y → X bền hơn Y.
Hai hạt nhân X và Y có độ hụt khối bằng nhau và số nuclôn của hạt nhân X nhỏ hơn số nuclôn của hạt nhân Y thì
A. năng lượng liên kết của hạt nhân X lớn hơn năng lượng liên kết của hạt nhân Y
B. hạt nhân X bền vững hơn hạt nhân Y
C. năng lượng liên kết riêng của hai hạt nhân bằng nhau
D. hạt nhân Y bền vững hơn hạt nhân X
Chọn đáp án B
Độ hụt khối bằng nhau → Wlkbằng nhau → Wlkr của X lớn hơn Y → X bền hơn Y
Hạt nhân C 6 12 có khối lượng hạt nhân là 11,9967 u. Cho m n = 1 , 008665 u ; m p = 1 , 007272 u . Độ hụt khối của hạt nhân đó là
A. 0,989464 u
B. 0,098922 u
C. 0,998946 u
D. 0,0098994 u
Giả sử hai hạt nhân X và Y có độ hụt khối bằng nhau, số nuclôn của hạt nhân X lớn hơn số nuclôn của hạt nhân Y thì
A. hạt nhân Y bền vững hơn hạt nhân X.
B. năng lượng liên kết của hạt nhân X lớn hơn năng lượng liên kết của hạt nhân Y.
C. năng lượng liên kết riêng của hai hạt nhân bằng nhau.
D. hạt nhân X bền vững hơn hạt nhân Y
Phương pháp: Năng lượng liên kết riêng càng lớn hạt nhân càng bền vững
Năng lượng liên kết : Wlk = ∆m.c2
Năng lượng liên kết riêng : ε = Wlk/A
Cách giải:
Do: ∆mX = ∆mY => WlkX = WlkY
Ta có :
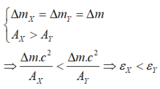
=> hạt nhân Y bền vững hơn hạt nhân X
Đáp án A