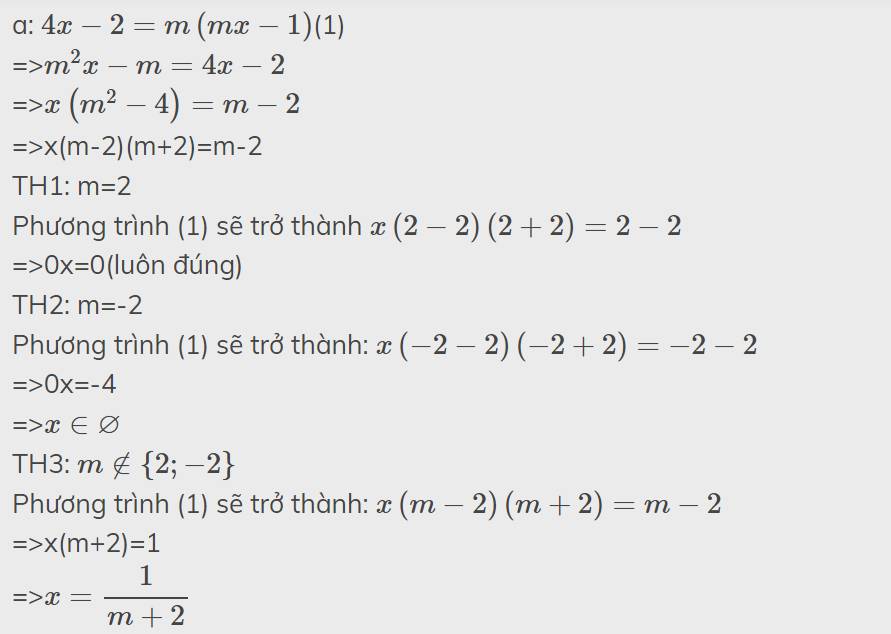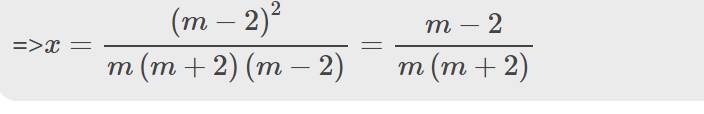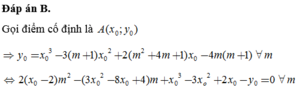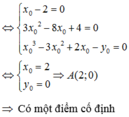(8m+4)/3*(4m+2)/3=m2+1
tìm m

Những câu hỏi liên quan
Phân tích đa thức thành nhân tử
8m + m4 - 8m2 - 4m3
Cho hệ phương trình (m+1)x +8y =4m
mx + (m+3)y=3m-1
Tìm m để hệ phương trình có nghiệm duy nhất
Phân tích đa thức thành nhân tử
8m + m4 - 8m2 - 4m3
\(=m\left(m^3-4m^2-8m+8\right)\)
\(=m\left[\left(m+2\right)\left(m^2-2m+4\right)-4m\left(m+2\right)\right]\)
\(=m\left(m+2\right)\left(m^2-6m+4\right)\)
Đúng 0
Bình luận (0)
Cho hệ phương trình (m+1)x +8y =4m
mx + (m+3)y=3m-1
tìm m nguyên để hpt có nghiệm duy nhất (x;y) thỏa mãn x,y ϵ Z
tìm m để phương trình (m2-1)x+2=m-1 nhận x-2 là nghiệm
Tìm m để pt 3x2+4mx=8 có nghiệm x=-1
Tìm m để pt (2m+3)x-5-(m+2)-x có nghiệm là x=3
Gig gấp vs các bạn !!!
Kiểm tra giúp mình yêu cầu thứ nhất nhé!
Có thể bạn tìm:
"Đề: Tìm m để phương trình (m2-1)x+2=m-1 nhận x=2 là nghiệm.
Giải: Thế x=2 vào phương trình đã cho, ta suy ra (m2-1).2+2=m-1 (vô nghiệm).
Không có giá trị nào của m để phương trình đã cho nhận x=2 là nghiệm. -Hết-".
Thế x=-1 vào phương trình đã cho, ta suy ra 3.(-1)2+4m.(-1)=8 \(\Rightarrow\) m=-5/4.
Bạn xem giúp mình yêu cầu cuối cùng nha!
Có thể bạn tìm:
"Đề: Tìm m để phương trình (2m+3)x-5=(m+2)-x có nghiệm là x=3.
Giải: Thế x=3 vào phương trình đã cho, ta suy ra (2m+3).3-5=(m+2)-3 \(\Rightarrow\) m=-1. -Hết-".
Đúng 0
Bình luận (0)
Giải và biện luận các phương trình sau
a) 4x-2=m(mx-1)
f) m2x-3=4x-(m-1)
g)m3x-4=m2+4mx-4m
Giải và biện luận các phương trình sau
a) 4x-2=m(mx-1)
f) m2x-3=4x-(m-1)
g)m3x-4=m2+4mx-4m
a: \(4x-2=m\left(mx-1\right)\)(1)
=>\(m^2x-m=4x-2\)
=>\(x\left(m^2-4\right)=m-2\)
=>x(m-2)(m+2)=m-2
TH1: m=2
Phương trình (1) sẽ trở thành \(x\left(2-2\right)\left(2+2\right)=2-2\)
=>0x=0(luôn đúng)
TH2: m=-2
Phương trình (1) sẽ trở thành: \(x\left(-2-2\right)\left(-2+2\right)=-2-2\)
=>0x=-4
=>\(x\in\varnothing\)
TH3: \(m\notin\left\{2;-2\right\}\)
Phương trình (1) sẽ trở thành: \(x\left(m-2\right)\left(m+2\right)=m-2\)
=>x(m+2)=1
=>\(x=\dfrac{1}{m+2}\)
f: \(m^2x-3=4x-\left(m-1\right)\)(2)
=>\(m^2x-4x=-m+1+3\)
=>\(x\left(m^2-4\right)=-m+2\)
=>\(x\left(m-2\right)\left(m+2\right)=-\left(m-2\right)\)
TH1: m=2
Phương trình (2) sẽ trở thành: \(x\left(2-2\right)\left(2+2\right)=-\left(2-2\right)\)
=>0x=0(luôn đúng)
TH2: m=-2
Phương trình (2) sẽ trở thành: \(x\left(-2-2\right)\left(-2+2\right)=-\left(-2-2\right)\)
=>0x=4
=>\(x\in\varnothing\)
TH3: \(m\notin\left\{2;-2\right\}\)
Phương trình (2) sẽ là: x(m-2)(m+2)=-(m-2)
=>x(m+2)=-1
=>\(x=-\dfrac{1}{m+2}\)
g: \(m^3x-4=m^2+4mx-4m\)(3)
=>\(m^3x-4mx=m^2-4m+4\)
=>\(x\left(m^3-4m\right)=\left(m-2\right)^2\)
=>\(x\cdot m\cdot\left(m+2\right)\left(m-2\right)=\left(m-2\right)^2\)
TH1: m=2
Phương trình (3) sẽ trở thành: \(x\cdot2\cdot\left(2+2\right)\left(2-2\right)=\left(2-2\right)^2\)
=>0x=0(luôn đúng)
TH2: m=0
Phương trình (3) sẽ trở thành:
\(x\cdot0\cdot\left(0+2\right)\left(0-2\right)=\left(0-2\right)^2\)
=>0x=4
=>\(x\in\varnothing\)
TH3: m=-2
Phương trình (3) sẽ trở thành;
\(x\cdot\left(-2\right)\left(-2+2\right)\left(-2-2\right)=\left(-2-2\right)^2\)
=>0x=16
=>\(x\in\varnothing\)
TH4: \(m\notin\left\{0;2;-2\right\}\)
Phương trình (3) sẽ trở thành:
\(x\cdot m\left(m+2\right)\left(m-2\right)=\left(m-2\right)^2\)
=>\(x=\dfrac{\left(m-2\right)^2}{m\left(m+2\right)\left(m-2\right)}=\dfrac{m-2}{m\left(m+2\right)}\)
Đúng 1
Bình luận (0)
1. Miếng đất hình tam giác có cạnh đáy là 8m, nếu mở rộng đáy thêm 5 m thì diện tích tăng thêm 40 m2. Tính diện tích miếng đất ban đầu.2. Miếng đất hình tam giác có cạnh đáy là 8m, nếu mở rộng đáy thêm 3 m thì diện tích tăng thêm 12 m2. Tính diện tích miếng đất ban đầu.3. Miếng đất hình tam giác có cạnh đáy là 8m, nếu mở rộng đáy thêm 2,5 m thì diện tích tăng thêm 10 m2. Tính diện tích miếng đất ban đầu.4. Miếng đất hình tam giác có cạnh đáy là 12,5m, nếu mở rộng đáy thêm 3 m thì diện tích tăng...
Đọc tiếp
1. Miếng đất hình tam giác có cạnh đáy là 8m, nếu mở rộng đáy thêm 5 m thì diện tích tăng thêm 40 m2. Tính diện tích miếng đất ban đầu.
2. Miếng đất hình tam giác có cạnh đáy là 8m, nếu mở rộng đáy thêm 3 m thì diện tích tăng thêm 12 m2. Tính diện tích miếng đất ban đầu.
3. Miếng đất hình tam giác có cạnh đáy là 8m, nếu mở rộng đáy thêm 2,5 m thì diện tích tăng thêm 10 m2. Tính diện tích miếng đất ban đầu.
4. Miếng đất hình tam giác có cạnh đáy là 12,5m, nếu mở rộng đáy thêm 3 m thì diện tích tăng thêm 15 m2. Tính diện tích miếng đất ban đầu.
5. Miếng đất hình thang có đáy lớn là 8m, đáy bé là 6m, nếu mở rộng đáy lớn thêm 2 m thì diện tích tăng thêm 18 m2. Tính diện tích miếng đất ban đầu.
6. Miếng đất hình thang có đáy lớn là 18m, đáy bé là 12m, nếu mở rộng đáy lớn thêm 3 m thì diện tích tăng thêm 18 m2. Tính diện tích miếng đất ban đầu.
Số điểm cố định của đồ thị hàm số
y
x
3
−
3
(
m
+
1
)
x
2
+
2
(
m
2
+
4
m
+
1
)
x
−
4
m
(
m
+
1
)
khi m thay đổi là: A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Số điểm cố định của đồ thị hàm số y = x 3 − 3 ( m + 1 ) x 2 + 2 ( m 2 + 4 m + 1 ) x − 4 m ( m + 1 ) khi m thay đổi là:
A. 0
B. 1
C. 2
D. 3
Đáp án B.
Gọi điểm cố định là A ( x 0 ; y 0 )
⇒ y 0 = x 0 3 − 3 ( m + 1 ) x 0 2 + 2 ( m 2 + 4 m + 1 ) x 0 − 4 m ( m + 1 ) ∀ m
⇔ 2 ( x 0 − 2 ) m 2 − ( 3 x 0 2 − 8 x 0 + 4 ) m + x 0 3 − 3 x o 2 + 2 x 0 − y 0 = 0 ∀ m
⇔ x 0 − 2 = 0 3 x 0 2 − 8 x 0 + 4 = 0 x 0 3 − 3 x 0 2 + 2 x 0 − y 0 = 0 ⇔ x 0 = 2 y 0 = 0 ⇒ A ( 2 ; 0 )
=>Có một điểm cố định
Đúng 0
Bình luận (0)
Số điểm cố định của đồ thị hàm số
y
x
3
−
3
(
m
+
1
)
x
2
+
2
(
m
2
+
4
m
+
1
)
x
−
4
m
(
m
+
1
)
khi m thay đổi là: A. 0 B. 1 C. 2 D. 3
Đọc tiếp
Số điểm cố định của đồ thị hàm số y = x 3 − 3 ( m + 1 ) x 2 + 2 ( m 2 + 4 m + 1 ) x − 4 m ( m + 1 ) khi m thay đổi là:
A. 0
B. 1
C. 2
D. 3