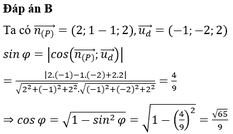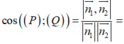Tính góc giữa hai mặt phẳng (P1): x + y + 2z – 1 = 0 và (P2): 2x – y + z – 2 = 0.

Những câu hỏi liên quan
Lập phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng
( P 1 ): 2x + y + 2z + 1 = 0 và ( P 2 ): 2x + y + 2z + 5 = 0.
Ta có: M(x, y, z) ∈ (P)
⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
⇔|2x + y + 2z + 1| = |2x + y + 2z + 5|
⇔ 2x + y + 2z + 1 = – (2x + y + 2z + 5)
⇔ 2x + y + 2z + 3 = 0
Từ đó suy ra phương trình của (P) là: 2x + y + 2z + 3 = 0.
Đúng 0
Bình luận (0)
Cho hai mặt phẳng:(
P
1
): 2x + y + 2z + 1 0 và (
P
2
): 4x – 2y – 4z + 7 0.Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến (
P
1
) và (
P
2
) là bằng nhau.
Đọc tiếp
Cho hai mặt phẳng:
( P 1 ): 2x + y + 2z + 1 = 0 và ( P 2 ): 4x – 2y – 4z + 7 = 0.
Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến ( P 1 ) và ( P 2 ) là bằng nhau.
Ta có: M(x, y, z) ∈ (P) ⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
![]()
⇔ 2|2x + y + 2z + 1| = |4x − 2y − 4z + 7|
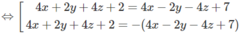
![]()
Từ đó suy ra phương trình mặt phẳng phải tìm là: 4y + 8z – 5 = 0 hoặc 8x + 9 = 0
Đúng 0
Bình luận (0)
Cho mặt phẳng
P
:
x
-
2
y
+
z
+
5
0
, Viết phương trình mặt phẳng (α) vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng
P
1
:
x
-
2
z
0
và
P
2
:
...
Đọc tiếp
Cho mặt phẳng P : x - 2 y + z + 5 = 0 , Viết phương trình mặt phẳng (α) vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
A. (α): 11x-2y-15z+3=0
B. (α): 11x+2y-15z-3=0
C. (α): 11x-2y+15z-3=0
D. (α): 11x-2y-15z-3=0
Chọn D
Từ phương trình hai mặt phẳng (P1), (P2) cho z = 1 ta tìm được điểm A(2;2;1) thuộc mặt phẳng (α) Tìm vecto chỉ phương của đường thẳng d. Vecto pháp tuyến của mặt phẳng cần tìm là tích có hướng của vecto pháp tuyến (P) và vecto chỉ phương của d
Đúng 0
Bình luận (0)
Cho mặt phẳng (P): x-2y+z+50. Viết phương trình mặt phẳng
α
vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng
P
1
:
x
-
2
z
0
và
P
2
:
3
x
-
2
y
+
z
-
3
0
Đọc tiếp
Cho mặt phẳng (P): x-2y+z+5=0. Viết phương trình mặt phẳng α vuông góc với mặt phẳng (P) và chứa đường thẳng d là giao của hai mặt phẳng P 1 : x - 2 z = 0 và P 2 : 3 x - 2 y + z - 3 = 0
![]()
![]()
![]()
![]()
Trong không gian Oxyz, cho hai đường thẳng
△
:
x
-
1
-
2
y
+
2
1
z
-
3
2
và mặt phẳng (P): x+y-2z+60. Góc giữa đường thẳng
△
với mặt phẳng (P) bằn...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng △ : x - 1 - 2 = y + 2 1 = z - 3 2 và mặt phẳng (P): x+y-2z+6=0. Góc giữa đường thẳng △ với mặt phẳng (P) bằng
A. 30 °
B. 45 °
C. 60 °
D. 135 °
Trong không giam Oxyz, cho mặt phẳng (P) có phương trình 2x-y+2z+10, đường thẳng d có phương trình
x
-
1
-
1
y
-
2
z
+
2
2
. Gọi
φ
là góc giữa đường thẳng d và mặt phẳng (P). Tính giá trị cos...
Đọc tiếp
Trong không giam Oxyz, cho mặt phẳng (P) có phương trình 2x-y+2z+1=0, đường thẳng d có phương trình x - 1 - 1 = y - 2 = z + 2 2 . Gọi φ là góc giữa đường thẳng d và mặt phẳng (P). Tính giá trị cos φ
A. cos φ = 6 / 9
B. cos φ = 65 9
C. cos φ = 9 65 65
D. cos φ = 4 / 9
Tính khoảng cách h giữa hai mặt phẳng song song:
P
:
2
x
-
y
+
2
z
-
1
0
và
Q
:
2
x
-
y
+
2
z
+
1
0
.
Đọc tiếp
Tính khoảng cách h giữa hai mặt phẳng song song: P : 2 x - y + 2 z - 1 = 0 và Q : 2 x - y + 2 z + 1 = 0 .
![]()
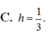
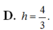
Trong không gian Oxyz cho hai mặt phẳng (P): 2x - y - 2z - 9 0, (Q): x - y - 6 0 Góc giữa hai mặt phẳng (P),(Q) bằng A.
90
o
B.
30
o
C.
45
o
D.
60
o
Đọc tiếp
Trong không gian Oxyz cho hai mặt phẳng (P): 2x - y - 2z - 9 = 0, (Q): x - y - 6 = 0 Góc giữa hai mặt phẳng (P),(Q) bằng
A. 90 o
B. 30 o
C. 45 o
D. 60 o
Trong không gian Oxyz, cho hai mặt phẳng (P): x+y-z+50 và (Q): 2x+2y-2z+30 Khoảng cách giữa và bằng
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng (P): x+y-z+5=0 và (Q): 2x+2y-2z+3=0 Khoảng cách giữa và bằng
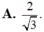
![]()
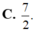
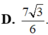
Trong không gian Oxyz, cho hai mặt phẳng
P
:
x
+
y
-
z
+
5
0
và
Q
:
2
x
+
2
y
-
2
z
+
3
0
. Khoảng cách giữa
y
1
x
2
+...
Đọc tiếp
Trong không gian Oxyz, cho hai mặt phẳng P : x + y - z + 5 = 0 và Q : 2 x + 2 y - 2 z + 3 = 0 . Khoảng cách giữa y = 1 x 2 + 3 P và Q bằng
A. 2 3
B. 2
C. 7 2
D. 7 3 6