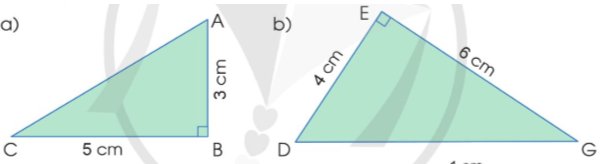
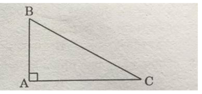
Tính diện tích các hình tam giác vuông sau:
Những câu hỏi liên quan
Hình thang ABCD và hình tam giác BEC có các số đo như sau: AB= 21,5 cm; DC= 334,6cm; CE= 4,8cm; diện tích hình tam giác BCE= 43,2cm vuông. Tính diên tích hình thang ABCD.
Tính diện tích hình tam giác vuông (theo công thức):Diện tích hình tam giác vuông là:Diện tích hình tam giác ABC là: ………………………
Đọc tiếp
Tính diện tích hình tam giác vuông (theo công thức):
Diện tích hình tam giác vuông là:
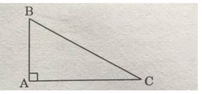
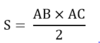
Diện tích hình tam giác ABC là: ………………………
Diện tích hình tam giác ABC là:
3 × 4 : 2 = 6 ( c m 2 )
Đúng 0
Bình luận (0)
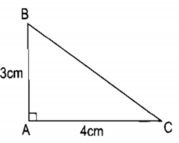
Bài giải
Diện tích hình tam giác đó là :
4 x 3 : 2 = 6 ( cm2 )
Đ/s : 6 cm2 .
Tính diện tích hình tam giác vuông (theo công thức):Diện tích hình tam giác vuông là: Diện tích hình tam giác DEG là:……………………………….
Đọc tiếp
Tính diện tích hình tam giác vuông (theo công thức):
Diện tích hình tam giác vuông là:
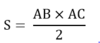
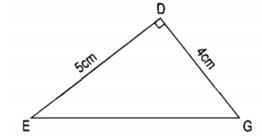
Diện tích hình tam giác DEG là:……………………………….
Diện tích hình tam giác DEG là:
5 × 4 : 2 = 10 ( c m 2 )
Đúng 0
Bình luận (0)
Cho hình thang ABCD có AB // CD, O là giao điểm của 2 đường chéo. Biết diện tích tam giác AOB bằng 9cm vuông, diện tích tam giác COD bằng 16cm vuông.
a) Tính diện tích các tam giác AOD, BOC.
b) Tính diện tích hình thang ABCD.
Các đường chéo của hình thang chia nó thành bốn tam giác, diện tích của các tam giác có một cạnh là đáy của hình thang là 4 cm vuông và 12 cm vuông. Tính diện tích hình thang đó
Tính tổng diện tích tất cả các tam giác có trong hình vẽ. Biết diện tích hình vuông đã cho là 156,25.
Trả lời: Tổng diện tích tất cả các tam giác có trong hình vẽ là
Cho hình vuông ABCD cạnh 12cm. Các điểm M, N lần lượt trên các cạnh AB, AD sao cho AM = DN = x.
a) Tính diện tích tam giác AMN theo x.
b) Tìm x để diện tích tam giác AMN bằng 1 9 diện tích hình vuông ABCD
Cho hình thang ABCD có AB // CD, O là giao điểm của 2 đường chéo. Biết diện tích tam giác AOB bằng 9cm vuông, diện tích tam giác COD bằng 16cm vuông.
a) Tính diện tích các tam giác AOD, BOC.
b) Tính diện tích hình thang ABCD.
Giúp mik vs ạ
Cho hình thang ABCD.NỐI A với C , B với D.Hỏi:
A:hãy chỉ ra các tam giác có diện tích bằng nhau
B:biết diện tích tam giác AOB là 40 cm vuông , diện tích tam giác ODC là 90 cm vuông, tính diện tích hình thang ABCD
Cho tam giác ABC vuông ở A và có BC = 2 AB = 2a. Ở phía ngoài tam giác, ta vẽ hình vuông BCDE, tam giác đều ABF và tam giác đều ACG
a) Tính các góc B, C cạnh AC và diện tích tam giác ABC
b) Chứng minh rằng FA vuông góc với BE và CG. Tính diện tích các tam giác FAG và FBE
c) Tính diện tích tứ giác DEFG
a) Giả sử M là trung điểm của BC, \(\Delta ABM\) là tam giác đều nên \(\widehat{ABC}=60^o.\)
Từ đó suy ra: \(\widehat{BCA}=30^o\). Theo định lí Py-ta-go, ta có:
AC = \(\sqrt{BC^2-AB^2}\)
AC = \(\sqrt{4a^2-a^2}=a\sqrt{3}.\)
Do đó, ta có:
SABC = \(\dfrac{1}{2}AB.AC=\dfrac{1}{2}a^2\sqrt{3}.\) (1)
b) Vì \(\widehat{FAB}=\widehat{ABC}=60^o\) nên FA // BC (hai góc so le trong), từ đó suy ra FA vuông góc với BE và CG.
Gọi giao điểm của FA và BE là H, giao điểm của FA và CG là K. Ta có:
SFAG = \(\dfrac{1}{2}FA.GK=\dfrac{1}{2}a.\dfrac{a\sqrt{3}}{2}=\dfrac{1}{4}a^2\sqrt{3},\) (2)
SFBE = \(\dfrac{1}{2}BE.FH=\dfrac{1}{2}.2a.\dfrac{a}{2}=\dfrac{1}{2}a^2.\) (3)
c) SBDCE = 4a2, (4)
SABF = \(\dfrac{1}{4}a^2\sqrt{3},\) (5)
SACG = \(\dfrac{3}{4}a^2\sqrt{3}.\) (6)
Từ (1), (2), (3), (4), (5), (6), ta có:
SDEFG = \(\dfrac{a^2}{4}\left(18+7\sqrt{3}\right)\approx7,53a^2.\)
Đúng 0
Bình luận (0)
