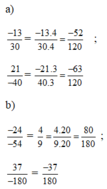a) 11^n − 1^n = 1330

Những câu hỏi liên quan
Tìm x; y biết : 2^x +1330 = 11^y
Cho n điểm ( n thuộc N, n lớn hơn hoặc bằng 3 ) trong đó không có 3 điểm nào thẳng hàng. Có 1330 tam giác mà các đỉnh là 3 trong n đỉnh đó. Tìm n
Tìm x;y là số TN biết: 2x+1330=11y
Ta có 11y luôn có chữ số tận cùng là 1 với mọi y thuộc N
và 1330 có tận cùng là 0
Do đó 2x có tận cùng là 1
=> x chỉ có thể bằng 0 (vì x thuộc N)
Ta có:
20 + 1330 = 11y
=> 1 + 1330 = 11y
=> 11y = 1331
=> 11y = 113
Vậy x = 0; y = 3
Đúng 0
Bình luận (0)
Chứng minh m chia hết cho 1997
\(\frac{m}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{1329}-\frac{1}{1330}+\frac{1}{1331}\)
\(\frac{m}{n}=\left(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{1331}\right)-\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{1330}\right)\)
\(\frac{m}{n}=\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{1330}+\frac{1}{1331}\right)-2.\left(\frac{1}{2}+\frac{1}{4}+...+\frac{1}{1330}\right)\)
\(\frac{m}{n}=\left(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{1330}+\frac{1}{1331}\right)-\left(1+\frac{1}{2}+...+\frac{1}{665}\right)\)
\(\frac{m}{n}=\frac{1}{666}+\frac{1}{667}+...+\frac{1}{1330}+\frac{1}{1331}\)
\(\frac{m}{n}=\left(\frac{1}{666}+\frac{1}{1331}\right)+\left(\frac{1}{667}+\frac{1}{1330}\right)+...+\left(\frac{1}{998}+\frac{1}{999}\right)\)
\(\frac{m}{n}=\frac{1997}{666.1331}+\frac{1997}{667.1330}+...+\frac{1997}{998.999}=\frac{1997k_1+1997.k_2+...+1997.k_{333}}{666.667...1331}\)
\(\frac{m}{n}=\frac{1997.\left(k_1+k_2+...+k_{333}\right)}{666.667...1330.1331}\) trong đó: k1;...; k333 là các thừa số phụ của các phân số trong tổng
Nhận xét: phân số trên có tử chia hết cho 1997 là số nguyên tố; mẫu số không chia hết cho thừa số nguyên tố 1997 nên khi rút gọn tử vẫn chia hết cho 1997
=> m chia hết cho 1997
Đúng 0
Bình luận (0)
Cho n điểm ( n thuộc N, n lớn hơn hoặc bằng 3 ) trong đó không có 3 điểm nào thẳng hàng. Có 1330 tam giác mà các đỉnh là 3 trong n đỉnh đó. Tìm n
Có 5 tế bào sinh dưỡng cừng loài nguyên phân một số lần bằng nhau và đã sử dụng của môi trường nguyên liệu tương đương 1330 NST. Tất cả các tế bào con được tạo ra sau nguyên phân chứa tổng số 1520 NST . Số lần nguyên phân củ mỗi tế bào nói trê là bao nhiêu?
+ Gọi số lần nguyên phân của mỗi TB là k
+ Bộ NST lưỡng bội 2n
+ Số NST môi trường cung cấp cho quá trình NP là:
5 . 2n . (2k - 1) = 1330 NST (1)
+ Tổng số NST chứa ở tất cả các TB con sau NP là:
5 . 2n . 2k = 1520 NST (2)
+ Từ 1 và 2 ta có: 2n = 38 và k = 3
Đúng 0
Bình luận (1)
Số NST trong tế bào con: 5.2n.2x = 1520 (1)
Số NST môi trường cung cấp:
NSTcc = 5.2n.(2x - 1) = 1330 (2)
(1)(2) <=> 2n = 38, x = 3
Sinh học 12 trên Youtube (Youtube -> tahava sẽ có video + bài tập + đáp án) hy vọng sẽ cải thiện tình hình học Môn Sinh của em. Chúc em học tốt!
Đúng 0
Bình luận (3)
Quy đồng mẫu các phân số sau
a) - 13 30 và 21 - 40
b) - 24 - 54 và 37 - 180
2xX+X+X+Xx3=1330
2xX+X+X+Xx3=1330
X(1+1+2+3)=1330\
X.7=1330
x=1330:7
x=190
Vậy x=190
Đúng 0
Bình luận (0)
2xX+X+X+Xx3=1330
2X+1X+1X+3X =1330 (bước này làm để bạn hiểu bước ở dưới)
(2+1+1+3)X =1330
7X = 1330
X = 1330:7
X = 190
Vậy X = 190
Chọn nha
Đúng 0
Bình luận (0)
giúp mik bài này nha
Chứng minh rằng số A=111..11(n số)2111...11(n số 1) là hợp số n>=1Chứng minh rằng số A=111..11(n số)2111...11(n số 1) là hợp số với n>=1
Đặt 111....1 ( n số 1 ) = a
=> 211....1( n số 1) = 2.1000....0( n số 0) + a = 2.(9a+1)+a = 18a+2+a = 19a+2
=> A = a+19a+2 = 20a+2 = 2.(10a+1) chia hết cho 2
Mà A > 2 => A là hợp số
=> ĐPCM
k mk nha
Đúng 0
Bình luận (0)
Chứng minh rằng :
a)với mọi n thuộc N thì A=8*n+11..11 chia hết cho 9 (11...111 có n chữ số 1 )
b)Với mọi a,b,n thuộc N thì B=(10n-1)*a+(11..111-n)*b chia hết cho 9 (111..111 có n chữ số 1)
c)888...88-9=n chia hết cho 9 (888..888 có n chữ số 8)