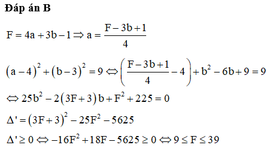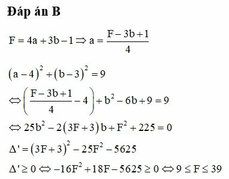Cho a, b thuộc R sao cho ab = 1 và Ia+bI đạt giá trị nhỏ nhất. Tính giá trị của biểu thức A= 3a^2 - 2a + 3b^2 - 2b + 6IaI + 1 ( chữ I I là dấu GTTĐ nha các bạn tại mình ko biết gõ nó ở đâu)

Những câu hỏi liên quan
cho a,b thuộc R sao cho ab=1 và Ia+bI đạt giá trị bé nhất. tính già trị của biểu thức A= 3a^2 - 2a + 3b^2 - 2b + 6IaI +1
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 0
Bình luận (0)
1.Biết a-2b=5, hãy tính giá trị của biểu thức :P=(3a-2b)/(2a+5)+(3b-a)/(b-5)
2.Cho a+b+c=0.Tính giá trị của các biểu thức sau:
A=1/(a^2+b^2-c^2)+1/(b^2+c^2-a^2)+1/(c^2+a^2-b^2)
P=3a-2b\2a+5 + 3b-a\b-5
=2a+a-2b\2a-5 + -a+2b+b\b-5
=2a+(a-2b)\2a-5 + -(a-2b)+b
=2a+5\2a-5 + -5+b\b-5
=-(2a-5)\(2a-5) + (b-5)\(b-5)
=-1+1=0
Đúng 0
Bình luận (0)
Cho số phức z thỏa mãn
z
-
1
+
3
i
+
z
¯
+
5
+
i
2
65
. Giá trị nhỏ nhất của
z
+
2
+
i...
Đọc tiếp
Cho số phức z thỏa mãn z - 1 + 3 i + z ¯ + 5 + i = 2 65 . Giá trị nhỏ nhất của z + 2 + i đạt được khi z = a + b i với a, b là các số thực dương. Giá trị của 2 b + 3 a bằng
A. 19
B. 16
C. 24
D. 13
Chọn đáp án B.
Cách 1: (Sử dụng kiến thức Hình học)
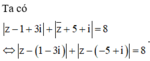
Gọi M, A, B, I lần lượt là điểm biểu diễn cho các số phức
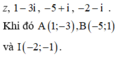
Có I là trung điểm của đoạn thẳng AB và

Áp dụng bất đẳng thức Cô-si, ta có


Cách 2: (Sử dụng kiến thức Đại số)
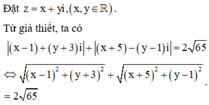
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xky, ta có
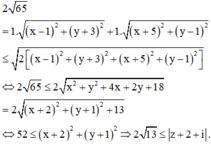
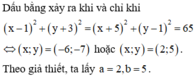

Đúng 0
Bình luận (0)
Cho a,b là 2 số thực dương thoả mãn a+b=2. Tìm giá trị nhỏ nhất của biểu thức
\(P=\frac{2a^2+3b^2}{2a^3+3b^3}+\frac{2b^2+3a^2}{2b^3+3a^3}\)
Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
\(M=a^2+ab+b^2-3a-3b+2001\)
\(\Rightarrow2M=2a^2+2ab+2b^2-6a-6b+4002\)
\(=\left(a^2+2ab+b^2\right)-4\left(a+b\right)+4+\left(a^2-2a+1\right)+\left(b^2-2b+1\right)+3996\)
\(=\left(a+b-2\right)^2+\left(a-1\right)^2+\left(b-1\right)^2+3996\ge3996\)
\(\Rightarrow M\ge1998\)
Đúng 0
Bình luận (0)
Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
Với các bài toán tìm max, min 2 biến kiểu như thế này, em hay cố gắng nhân M lên n lần để tạo thêm được các số hạng, sang đó ghép tạo thành các bình phương.
Cách làm như sau:
\(4M=4a^2+4ab+4b^2-12a-12b+8004\)
\(=\left(4a^2+4ab+b^2\right)-6\left(2a+b\right)+3\left(b^2-2b\right)+8004\)
\(=\left(2a+b\right)^2-6\left(2a+b\right)+9+3\left(b^2-2b+1\right)+7992\)
\(=\left(2a+b-3\right)^2+3\left(b-1\right)^2+7992\ge7992\)
Vậy 4M min = 7992, vây M min = 1998.
Vậy min M = 1998 khi \(\hept{\begin{cases}b-1=0\\2a+b-3=0\end{cases}}\Rightarrow\hept{\begin{cases}b=1\\a=1\end{cases}}\)
Đúng 0
Bình luận (0)
1 Cho biểu thức M a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.2 Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Đọc tiếp
1 Cho biểu thức M = a2 + ab + b2 – 3a – 3b + 2001. Với giá trị nào của a và b thì M đạt giá trị nhỏ nhất? Tìm giá trị nhỏ nhất đó.
2 Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
3 Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
2:
a: =>a^2+2ab+b^2-2a^2-2b^2<=0
=>-(a^2-2ab+b^2)<=0
=>(a-b)^2>=0(luôn đúng)
b; =>a^2+b^2+c^2+2ab+2ac+2bc-3a^2-3b^2-3c^2<=0
=>-(2a^2+2b^2+2c^2-2ab-2ac-2bc)<=0
=>(a-b)^2+(b-c)^2+(a-c)^2>=0(luôn đúng)
Đúng 0
Bình luận (0)
Cho số phức z= a+bi (a,b∈R). Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R=3. Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F=4a+3b-1. Tính giá trị M+ m.
A. M+ m=63
B. M+ m=48
C. M+ m=50
D. M+ m=41
Cho số phức
z
a
+
b
i
a
,
b
∈
R
Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R3 Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F 4a+3b-1 Tính giá trị M+m A. M + m 63 B. M + m 48 C. M + m 50 D. M + m 41
Đọc tiếp
Cho số phức z = a + b i a , b ∈ R Biết tập hợp các điểm A biểu diễn hình học số phức z là đường tròn (C) có tâm I(4;3) và bán kính R=3 Đặt M là giá trị lớn nhất, m là giá trị nhỏ nhất của F = 4a+3b-1 Tính giá trị M+m
A. M + m = 63
B. M + m = 48
C. M + m = 50
D. M + m = 41