Cho tam giác AOB có OA=OB,O1=O2 =AOB/2.Chứng tỏ OD vuông góc AB

Những câu hỏi liên quan
cho tam giác AOB ,biết OA=OB,góc O1=O2=AOB/2.Chứng minh OD vuông góc AB
Cho góc AOB có số đo là
130
0
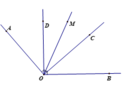
. Trong góc ấy vẽ các tia OC và OD sao cho OC vuông góc OA và OD vuông góc OB. a) Chứng tỏ rằng:
A
O
D
^
C
O
B
^
.b) Tính
D
O
C
^
.c) Gọi OM là phân...
Đọc tiếp
Cho góc AOB có số đo là
130
0
. Trong góc ấy vẽ các tia OC và OD sao cho OC vuông góc OA và OD vuông góc OB.
a) Chứng tỏ rằng:
A
O
D
^
=
C
O
B
^
.
b) Tính
D
O
C
^
.
c) Gọi OM là phân giác của góc AOB. Hãy chứng tỏ rằng OM là tia phân giác của
C
O
D
^

a. Ta có:
O A ⊥ O C ( G T ) ⇒ A O C ^ = 90 ° O D ⊥ O B ( G T ) ⇒ D O B ^ = 90 ° A O D ^ + C O D ^ = A O C ^ = 90 ° B O C ^ + C O D ^ = D O B ^ = 90 °
⇒ A O D ^ = B O C ^ (Cùng phụ C O D ^ )
b. Ta có:
A O D ^ + B O D ^ = A O B ^ ⇒ A O D ^ + 90 ° = 130 ° ⇒ A O D ^ = 130 ° − 90 ° ⇒ A O D ^ = 40 °
Mà A O D ^ + C O D ^ = 90 ° ( C M T )
40 ° + C O D ^ = 90 ° C O D ^ = 50 °
c. OM là tia phân giác của A O B ^ nên:
A O M ^ = B O M ^ = A O B ^ 2 = 65 °
A O D ^ + D O M ^ = A O M ^ 40 ° + D O M ^ = 65 ° D O M ^ = 25 °
Tương tự ta tìm được C O M ^ = 25 °
Do đó C O M ^ = D O M ^ ( = 25 ° )
Vậy OM là tia phân giác của C O D ^
Đúng 0
Bình luận (0)
Cho góc AOB là góc tù và tia OC, OD nằm trong góc AOB sao cho OC vuông góc OA, OD vuông góc OB. Chứng tỏ góc AOD= góc BOC
Lời giải:
Ta có:
$\widehat{AOD}+\widehat{DOC}=\widehat{AOC}=90^0$
$\widehat{BOC}+\widehat{DOC}=\widehat{BOD}=90^0$
$\Rightarrow \widehat{AOD}+\widehat{DOC}=\widehat{BOC}+\widehat{DOC}$
$\Rightarrow \widehat{AOD}=\widehat{BOC}$
$\
Đúng 2
Bình luận (0)
1. Cho AOB = 120 độ. Vẽ tia OC, OD nằm trong AOB sao cho OC vuông với OB và OD vuông với OA. Chứng tỏ AOC = BOD.
2. Cho MON bẹt. VẼ 3 tia OA, OB, OC trên cùng 1 nữa mặt phẳng có bờ là đường MN sao cho AOM = BON và tia OC là tia phân giác của AOB. Chứng tỏ OC vuông với MN.
cho tam giác AOB có OA=OB. Tia phân giác của góc O cắt AB tại D. chứng minh
a/ DA=DB
b/ OD vuông góc vs AB
a, xét tam giác AOD và tam giác BOD có:
OA=OB (gt)
góc AOD= góc BOD ( OD là phân giác góc O)
OD chung
suy ra: tam giác AOD= BOD ( c.g.c)
suy ra: DA=DB (hai cạnh tương ứng)
b, vì tam giác AOD=BOD (chứng minh trên)
suy ra: góc ADO=gócBDO (2 góc tương ứng)
mà góc ADO+BDO=180 độ ( kề bù)
suy ra: góc ADO=góc BDO=180/2=90 độ (t/c)
suy ra: OD vuông góc với AB tại D (t/c)
Đúng 0
Bình luận (0)
bài của bạn kacura giống bài bạn bạch cúc bên trên quá há
Cho tam giác AOB có OA = OB. Tia phân giác của góc O cắt AB tại D.
Chứng minh rằng:
a, DA = DB
b, OD vuông góc với AB
a, xét tam giác AOD và tam giác BOD có:
OA=OB (gt)
góc AOD= góc BOD ( OD là phân giác góc O)
OD chung
suy ra: tam giác AOD= BOD ( c.g.c)
suy ra: DA=DB (hai cạnh tương ứng)
b, vì tam giác AOD=BOD (chứng minh trên)
suy ra: góc ADO=gócBDO (2 góc tương ứng)
mà góc ADO+BDO=180 độ ( kề bù)
suy ra: góc ADO=góc BDO=180/2=90 độ (t/c)
suy ra: OD vuông góc với AB tại D (t/c)
Đúng 1
Bình luận (0)
Chúc bạn chơi game vui vẻ 🙂 và theo dõi tin tức game trên thegioigame.vn
Không vẽ hình (:
a) Xét tam giác OAD và OAB có :
OA = OB ( gt )
^AOD = ^BOD ( do OD là phân giác của ^O )
OD chung
=> Tam giác OAD = tam giác OAB ( c.g.c )
=> DA = DB ( hai cạnh tương ứng ) ( đpcm )
b) Tam giác OAD = tam giác OBD
=> ^ODA = ^ODB ( hai góc tương ứng ) ( 1 )
^ODA + ^ODB = 1800 ( kề bù ) ( 2 )
Từ ( 1 ) và ( 2 ) => ^ODA = ^ODB = 1800/2 = 90
=> OD vuông góc với AB ( đpcm )
Xem thêm câu trả lời
Cho tam giác AOB có OA=OB. Tia phân giác góc O cắt AB ở D.CMR DA=DB , OD vuông góc với AB
xét \(\Delta OAB\)là \(\Delta\)cân vì \(OA=OB\)( giả thiết)
và \(OD\)là tia phân giác \(\widehat{AOB}\)cắt \(AB\)TẠI \(D\)
\(\Rightarrow OD\)ĐỒNG THỜI LÀ ĐƯỜNG TRUNG TRỰC CỦA \(\Delta OAB\)
\(\Rightarrow AD=DB\) và \(OD\perp AB\)tại \(D\)( điều phải chứng minh)
vậy \(AD=DB\) và \(OD\perp AB\)
Đúng 1
Bình luận (0)
Cho tam giác AOB có OA=OB . Tia phân giác của góc O cắt AB ở D . a) Chứng minh ΔAOD=ΔBOD. b) Chứng minh OD AB. c) Đường vuông góc với OA tại A cắt đường vuông góc với OB tại B ở điểm E . Chứng minh OE là đường trung trực của đoạn thẳng AB.
a, xét tam giác ODA và tam giác ODB có : OD chung
^DOB = ^DOA do OD là pg của ^BOA (gt)
OA = OB (gt)
=> tam giác ODA = tam giác ODB (c-g-c)
b, t đoán đề là cm OD _|_ AB
tam giác ODA = tam giác ODB (câu a)
=> ^ODA = ^ODB (đn)
mà ^ODA + ^ODB = 180 (kb)
=> ^ODA = 90
=> OD _|_ AB
c, xét tam giác BOE và tam giác AOE có : OE chung
^BOD = ^AOD (câu a)
OB = AO (gt)
=> tam giác BOE = tam giác AOE (c-g-c)
=> EB = EA (đn) => E thuộc đường trung trực của AB
OB = OA (Gt) => O thuộc đường trung trực của AB
=> OE là trung trực của AB
Cho góc AOB bằng 130 độ. Trong góc AOB vẽ các tia OC, OD sao cho: OC vuông góc với OA, OD vuông góc với OB.
a) chứng tỏ AOD=BOC.
b)Tính góc COD.
c)Gọi OM là tia phân giác của COD, chứng tỏ OM là tia phân giác của AOB và ngược lại
a, Ta có
\(\widehat{AOD}=\widehat{AOB}-\widehat{BOD}\)
\(\Rightarrow\widehat{AOD}=130^0-90^0=40^0\) [ 1 ]
Mặt khác
\(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}\)
\(\Rightarrow\widehat{BOC}=130^0-90^0=40^0\) [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra
\(\widehat{AOD}=\widehat{BOC}=40^0\)
b.Ta thấy
\(\widehat{AOB}=\widehat{AOD}+\widehat{COD}+\widehat{BOC}\)
\(\Rightarrow\widehat{COD}=\widehat{AOB}-2\widehat{AOD}\)[ vì góc AOD = góc BOC theo câu a ]
\(\Rightarrow\widehat{COD}=130^0-2.40^0\)
\(\Rightarrow\widehat{COD}=130^0-80^0=50^0\)
Vậy góc COD = 50độ
c.Vì OM là tia phân giác góc COD nên
\(\widehat{COM}=\widehat{DOM}=\frac{\widehat{COD}}{2}=\frac{50^0}{2}=25^0\)
Ta có
\(\widehat{AOM}=\widehat{AOD}+\widehat{DOM}\)
\(\Rightarrow\widehat{AOM}=40^0+25^0=65^0\)
mà \(\widehat{BOM}=\widehat{BOC}+\widehat{COM}\)
\(\Rightarrow\widehat{BOM}=40^0+25^0=65^0\)
Suy ra \(\widehat{AOM}=\widehat{BOM}\)
Vậy OM là tia phân giác góc AOB
Chúc bạn học tốt






















