Question

Cho góc AOB có số đo là 130 0 . Trong góc ấy vẽ các tia OC và OD sao cho OC vuông góc OA và OD vuông góc OB.
a) Chứng tỏ rằng: A O D ^ = C O B ^ .
b) Tính D O C ^ .
c) Gọi OM là phân giác của góc AOB. Hãy chứng tỏ rằng OM là tia phân giác của  C O D ^

Answer 1

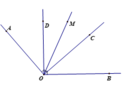
a. Ta có:

  O A ⊥ O C ( G T ) ⇒ A O C ^ = 90 ° O D ⊥ O B ( G T ) ⇒ D O B ^ = 90 ° A O D ^ + C O D ^ = A O C ^ = 90 ° B O C ^ + C O D ^ = D O B ^ = 90 °

⇒ A O D ^ = B O C ^ (Cùng phụ C O D ^ )

b. Ta có:

      A O D ^ + B O D ^ = A O B ^ ⇒ A O D ^ + 90 ° = 130 ° ⇒ A O D ^ = 130 ° − 90 ° ⇒ A O D ^ = 40 °

 Mà  A O D ^ + C O D ^ = 90 ° ( C M T )

40 ° + C O D ^ = 90 ° C O D ^ = 50 °

c. OM là tia phân giác của A O B ^  nên:

A O M ^ = B O M ^ = A O B ^ 2 = 65 °

A O D ^ + D O M ^ = A O M ^ 40 ° + D O M ^ = 65 ° D O M ^ = 25 °

Tương tự ta tìm được  C O M ^ = 25 °

Do đó  C O M ^ = D O M ^ ( = 25 ° )

Vậy OM là tia phân giác của  C O D ^