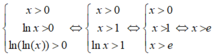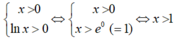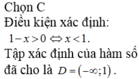Cho hàm số f(x) = lnx - ln(x + 1). Tìm tập xác định của hàm số trên.
Những câu hỏi liên quan
Tìm miền xác định của hàm số y = ln(ln(lnx))
A. D = (0; +∞)
B. D = (1; +∞)
C. D = (e; +∞)
D. D = ( e e ; + ∞ )
Tìm miền xác định của hàm số y = ln ( ln x )
A. D = (e; +∞)
B. D = [e; ∞)
C. D = (0; +∞)
D. D = (1; +∞)
Cho bốn hàm số sau : y f(x) lnx ;
y
g
(
x
)
2
x
2
+
4
;
y
h
(
x
)
2017
1018
x
và y l(x) ln( x2+1). Có bao nhiêu hàm số...
Đọc tiếp
Cho bốn hàm số sau : y= f(x) = lnx ; y = g ( x ) = 2 x 2 + 4 ; y = h ( x ) = 2017 1018 x và
y= l(x)= ln( x2+1). Có bao nhiêu hàm số đồng biến trên khoảng ( 0 ; + ∞ )
A. 1
B. 2
C. 3
D. 4
+ Sử dụng tính chất: Hàm số y= logax đồng biến trên TXĐ khi a> 1nên y= f(x) = lnx
là hàm số đồng biến.
+ Sử dụng tính chất: Hàm số y= ax nghịch biến trên R khi 0< a< 1nên
Chọn C
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số
y
ln
(
1
-
x
)
A. D
(
-
∞
;
-
1
)
B. D
(
-
1
;
+
∞
)
C. D
(
-
∞
;
1
)
D. D ...
Đọc tiếp
Tìm tập xác định của hàm số y = ln ( 1 - x )
A. D = ( - ∞ ; - 1 )
B. D = ( - 1 ; + ∞ )
C. D = ( - ∞ ; 1 )
D. D = ( 1 ; + ∞ )
Tìm tập xác định của hàm số y ln(1-x).
A
.
D
(
-
∞
;
-
1
)
B
.
D
(
1
;
+
∞
)
C
.
D
(
-
∞
;
1
)
D
....
Đọc tiếp
Tìm tập xác định của hàm số y = ln(1-x).
A . D = ( - ∞ ; - 1 )
B . D = ( 1 ; + ∞ )
C . D = ( - ∞ ; 1 )
D . D = ( 1 ; + ∞ )
Chọn C
Điều kiện xác định: 
Tập xác định của hàm số đã cho là D = ( - ∞ ; 1 )
Đúng 0
Bình luận (0)
Tìm tập xác định của hàm số
y
ln
(
1
-
x
)
2
.
A
.
(
1
;
+
∞
)
B
.
(
-
∞
;
1
)
C
.
ℝ
D...
Đọc tiếp
Tìm tập xác định của hàm số y = ln ( 1 - x ) 2 .
A . ( 1 ; + ∞ )
B . ( - ∞ ; 1 )
C . ℝ
D . ℝ \ { 1 }
Tìm tập xác định của hàm số
y
ln
(
1
-
x
)
2
A.
(
1
;
+
∞
)
B.
(
-
∞
;
1
)
C. R D. R {1}
Đọc tiếp
Tìm tập xác định của hàm số y = ln ( 1 - x ) 2
A. ( 1 ; + ∞ )
B. ( - ∞ ; 1 )
C. R
D. R \ {1}
Tìm tập xác định D của hàm số
y
ln
(
x
-
1
)
Đọc tiếp
Tìm tập xác định D của hàm số y = ln ( x - 1 )
Cho hai hàm số
y
e
x
và
y
ln
x
. Xét các mệnh đề sau (I) Đồ thị hai hàm số đối xứng qua đường thẳng yx(II) Tập xác định của hai hàm số trên là R (III) Đồ thị hai hàm số cắt nhau tại đúng một điểm. (IV) Hai hàm số đều đồng biến trên tập xác định của nó.Có bao nhiêu mệnh đề sai trong các mệnh đề trên? A. 2 B. 3 C. 1 D. 4
Đọc tiếp
Cho hai hàm số y = e x và y = ln x . Xét các mệnh đề sau
(I) Đồ thị hai hàm số đối xứng qua đường thẳng y=x
(II) Tập xác định của hai hàm số trên là R
(III) Đồ thị hai hàm số cắt nhau tại đúng một điểm.
(IV) Hai hàm số đều đồng biến trên tập xác định của nó.
Có bao nhiêu mệnh đề sai trong các mệnh đề trên?
A. 2
B. 3
C. 1
D. 4
Đáp án A
Các mệnh đề sai là (II) và (III)
Đúng 0
Bình luận (0)
SGK Kết nối tri thức và cuộc sống
15 tháng 8 2023 lúc 19:57
Tìm tập xác định của các hàm số sau:
a) \(y = \sqrt {{4^x} - {2^{x + 1}}} \)
b) \(y = \ln (1 - \ln x)\).
\(a,4^x-2^{x+1}\ge0\\ \Leftrightarrow2^{x+1}\le2^{2x}\\ \Leftrightarrow x+1\le2x\\ \Leftrightarrow x\ge1\)
Tập xác định của hàm số là D = \([1;+\infty)\)
\(b,\left\{{}\begin{matrix}x>0\\1-ln\left(x\right)>0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x>0\\ln\left(x\right)< 1\end{matrix}\right.\\ \Leftrightarrow0< x< e\)
Tập xác định của hàm số là \(\left(0;e\right)\)
Đúng 0
Bình luận (0)