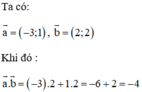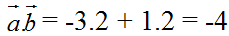Hãy nhắc lại công thức xác định tích vô hướng của hai vectơ trong mặt phẳng.

Những câu hỏi liên quan
Nhắc lại định nghĩa tích vô hướng của hai vectơ a→ và b→. Tích vô hướng này với |a→| và |b→| không đổi đạt giá trị lớn nhất và nhỏ nhất khi nào?
Tích vô hướng của hai vec tơ a→ và b→:
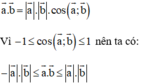
+ a→.b→ đạt giá trị lớn nhất bằng 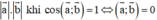 ⇔ a→ và b→ cùng hướng.
⇔ a→ và b→ cùng hướng.
+ a→.b→ đạt giá trị nhỏ nhất bằng 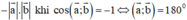 ⇔ a→ và b→ ngược hướng.
⇔ a→ và b→ ngược hướng.
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho vectơ a→(-3; 1) và b→(2; 2). Hãy tính tích vô hướng a→.b→.
Trong mặt phẳng tọa độ Oxy, cho hai vectơ
a
→
4
i
→
+
6
j
→
và
b
→
3
i
→
−
7
j
→
.
Tính tích vô hướng
a
→
.
b
→...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho hai vectơ a → = 4 i → + 6 j → và b → = 3 i → − 7 j → . Tính tích vô hướng a → . b → .
A. – 30
B. 3
C. 30
D. 43
Từ giả thiết suy ra a → = 4 ; 6 và b → = 3 ; − 7 .
Suy ra a → . b → = 4.3 + 6. − 7 = − 30.
Chọn A.
Đúng 0
Bình luận (0)
Nhắc lại định nghĩa tích vô hướng của hai vectơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\). Tích vô hướng này với \(\left|\overrightarrow{a}\right|\) và \(\left|\overrightarrow{b}\right|\) không đổi đạt giá trị lớn nhất và nhỏ nhất khi nào ?
Trong mặt phẳng tọa độ cho các vectơ
a
→
3
;
−
1
,
b
→
4
;
14
. Tích vô hướng
a
→
.
b
→
bằng A. 2 B. -2 C. 3 D. 1
Đọc tiếp
Trong mặt phẳng tọa độ cho các vectơ a → 3 ; − 1 , b → 4 ; 14 . Tích vô hướng a → . b → bằng
A. 2
B. -2
C. 3
D. 1
Đáp án B
a → . b → = 3.4 + − 1 .14 = − 2
Đúng 0
Bình luận (0)
Hai dây dẫn thẳng dài vô hạn đặt trong không khí vuông góc nhau (cách điện với nhau) và nằm trong cùng một mặt phẳng như hình vẽ. Cường độ dòng điện qua hai dây dẫn
I
1
2
A
;
I
2
10
A
.
a) Xác định cảm ứng từ gây bởi hai dòng điện tại M (x 5cm, y 4cm) trong mặt phẳng của hai dòng điệnb) Xác định những điểm có vectơ cảm ứng từ gây b...
Đọc tiếp
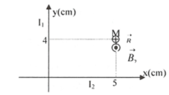
Hai dây dẫn thẳng dài vô hạn đặt trong không khí vuông góc nhau (cách điện với nhau) và nằm trong cùng một mặt phẳng như hình vẽ. Cường độ dòng điện qua hai dây dẫn I 1 = 2 A ; I 2 = 10 A .
a) Xác định cảm ứng từ gây bởi hai dòng điện tại M (x = 5cm, y = 4cm) trong mặt phẳng của hai dòng điện
b) Xác định những điểm có vectơ cảm ứng từ gây bởi hai dòng điện bằng 0.


b) Gọi N là điểm có vectơ cảm ứng từ gây bởi hai dòng điện bằng 0, ta có N phải thuộc góc phần tư thứ nhất và thứ ba
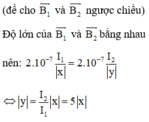
Vì N thuộc góc phần tư thứ nhất và thứ ba nên x, y cùng dấu, suy ra y = 5x
Vậy tập hợp những điểm có vectơ cảm ứng từ gây bởi hai dòng điện bằng 0 là đường thẳng y = 5x
Đúng 1
Bình luận (0)
Trong mặt phẳng Oxy cho vectơ \(\overrightarrow{a}=\left(-3;1\right)\) và vectơ \(\overrightarrow{b}=\left(2;2\right)\). Hãy tính tích vô hướng \(\overrightarrow{a}.\overrightarrow{b}\) ?
\(\overrightarrow{a}\) . \(\overrightarrow{b}\) = ( -3) . 2 + 1.2 = -4
Đúng 0
Bình luận (0)
Hãy nhắc lại công thức tính khoảng cách giữa 2 điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\)trong mặt phẳng Oxy.
Khoảng cách hai điểm M,I (hay độ dài đoạn thẳng MI) chính là độ dài vecto \(\overrightarrow {MI} \)
\(\overrightarrow {MI} = \left( {a - x;b - y} \right) \Rightarrow \left| {\overrightarrow {MI} } \right| = \sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
Vậy khoảng cách giữa hai điểm \(I\left( {a;b} \right)\) và \(M\left( {x;y} \right)\) là \(\sqrt {{{\left( {a - x} \right)}^2} + {{\left( {;b - y} \right)}^2}} \)
Đúng 0
Bình luận (0)
Trong không gian cho hai hình vuông ABCD và ABCD có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O. Hãy xác định góc giữa cặp vectơ
A
B
→
v
à
O
O
→
? A. ...
Đọc tiếp
Trong không gian cho hai hình vuông ABCD và ABC'D' có chung cạnh AB và nằm trong hai mặt phẳng khác nhau, lần lượt có tâm O và O'. Hãy xác định góc giữa cặp vectơ A B → v à O O ' → ?
A. 60 o
B. 45 o
C. 120 o
D. 90 o
Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có Mleft( {2;1} right),Nleft( { - 1;3} right),Pleft( {4;2} right)a) Tìm tọa độ của các vectơ overrightarrow {OM} ,overrightarrow {MN} ,overrightarrow {MP} b) Tính tích vô hướng overrightarrow {MN} .overrightarrow {MP} c) Tính độ dài các đoạn thẳng MN,MPd) Tính cos widehat {MNP}e) Tìm tọa độ trung điểm I của NP và trọn tâm G của tam giác MNP
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho tam giác MNP có \(M\left( {2;1} \right),N\left( { - 1;3} \right),P\left( {4;2} \right)\)
a) Tìm tọa độ của các vectơ \(\overrightarrow {OM} ,\overrightarrow {MN} ,\overrightarrow {MP} \)
b) Tính tích vô hướng \(\overrightarrow {MN} .\overrightarrow {MP} \)
c) Tính độ dài các đoạn thẳng \(MN,MP\)
d) Tính \(\cos \widehat {MNP}\)
e) Tìm tọa độ trung điểm I của NP và trọn tâm G của tam giác MNP
a) Ta có: \(\overrightarrow {OM} = \left( {2;1} \right),\overrightarrow {MN} = \left( { - 3;2} \right),\overrightarrow {MP} = \left( {2;1} \right)\)
b) Ta có: \(\overrightarrow {MN} .\overrightarrow {MP} = - 3.2 + 2.1 = - 4\)
c) Ta có: \(MN = \left| {\overrightarrow {MN} } \right| = \sqrt {{{\left( { - 3} \right)}^2} + {2^2}} = \sqrt {13} ,MP = \left| {\overrightarrow {MP} } \right| = \sqrt {{2^2} + {1^2}} = \sqrt 5 \)
d) Ta có: \(\cos \widehat {MNP} = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{\left| {\overrightarrow {MN} } \right|.\left| {\overrightarrow {MP} } \right|}} = \frac{- 4}{{\sqrt {13} .\sqrt 5 }} = \frac{- 4}{{\sqrt {65} }}\)
e) Tọa độ trung điểm I của đoạn NP là: \(\left\{ \begin{array}{l}{x_I} = \frac{{{x_N} + {x_P}}}{2} = \frac{3}{2}\\{y_I} = \frac{{{y_N} + {y_P}}}{2} = \frac{5}{2}\end{array} \right. \Leftrightarrow I\left( {\frac{3}{2};\frac{5}{2}} \right)\)
Tọa độ trọng tâm G của tam giác MNP là: \(\left\{ \begin{array}{l}{x_G} = \frac{{{x_M} + {x_N} + {x_P}}}{3}\\{y_G} = \frac{{{y_M} + {y_N} + {y_P}}}{3}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_G} = \frac{5}{3}\\{y_C} = 2\end{array} \right. \Leftrightarrow G\left( {\frac{5}{3};2} \right)\)
Đúng 0
Bình luận (0)