Cho tam giác ABC vuông tại A , trên tia đối của tia BC lấy điểm D, trên cạch BC lấy điểm E sao cho góc BAD = góc BAE . Chứng minh: BD.CE=CD.BE
Những câu hỏi liên quan
Tam giác ABC vuông tại A trên tia đối của BC lấy điểm D . Trên BC lấy điểm E sao cho góc BAD = góc BAE .chứng minh BD.CE = CD.BE
Cho tam giác ABC vuông tại A. Trên tia đối của tia BC lấy điểm D, trên cạnh BC lấy điểm E sao cho góc BAD bằng góc BAE. Chứng minh: BD.EC = CD.BE
cho tam giác abc vuông tại a. lấy d trên cạnh bc sao cho góc bad= góc bca. Trên tia đối của tia AD lấy điểm E sao cho AE= BC. Trên tia đối của tia CA lấy điểm F sao cho CF=AB. CHỨNG MINH BE VUÔNG GÓC BF
Có: Góc BAE + BAD = góc BCF + BCA (=180 độ)
Góc BAD = BCA
⇒ góc BAE = FCB
Xét △BAE và △FCB có:
AB = CF
BAE = FCB
AE = CB
⇒△BAE = △FCB (c.g.c)
⇒EBA = CFB
Mà góc CFB + ABF = 90 độ ⇒EBA + ABF = 90 độ
⇒ góc EBF = 90 độ ⇒BE vuông góc với BF
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A. Lấy điểm D trên cạnh BC sao cho góc BAD = góc BCA. Trên tia đối của tia AD lấy E sao cho AE=BC.Trên tia đối của tia CA lấy điểm F sao cho CF=AB. Chứng minh: BE vuông góc với BF
Cho tam giác ABC vuông tại A > lấy điểm D trên cạnh BC sao cho BAD=BCA
Trên tia đối của tia AD lấy điểm E sao cho AE=BC. Trên tia đối của tia CA lấy điểm F sao cho
CF=AB. Chứng minh : BE vuông góc với BF
Cho tam giác ABC vuông tại A. Lấy điểm D trên cạnh BC sao cho góc BAD= góc BCA. Trên tia đối của tia AD lấy E sao cho AE=BC.Trên tia đối của tia đối của tia CA lấy F sao cho CF=AB. Chứng minh BE vuông góc với BF?
Cho tam giác ABC vuông tại A. Trên BC lấy điểm E sao cho BA=BE. Tia phân giác của góc B cắt AC ở D. Trên BC lấy điểm E sao cho BA=BE
a) Chứng minh tam giác ABD= tam giác EBD
b) Chứng minh DE vuông góc với BC
c) Trên tia đối của tia AB lấy điểm M sao cho AM=EC, chứng minh MD=CD
a: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
b: Ta có: ΔBAD=ΔBED
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥BC
c: Xét ΔDEC vuông tại E và ΔDAM vuông tại A có
DE=DA
EC=AM
Do đó: ΔDEC=ΔDAM
Suy ra: DC=DM
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông tại A (AB AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm K sao cho BA BKa/ Chứng minh tam giác BAD BKD và b/ Trên tia đối của tia AB lấy điểm E sao cho BE BC. Gọi I là giao điểm của tia BD với CE. Chứng minh c/ Chứng minh ba điểm K, D, E thẳng hàng.Cần gấp. Chi tiết!!!!
Đọc tiếp
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc ABC cắt AC tại D. Trên cạnh BC lấy điểm K sao cho BA = BK
a/ Chứng minh tam giác BAD = BKD và format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%226.5%22%20y%3D%2216%22%3ED%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2217.5%22%20y%3D%2216%22%3EK%3C%2Ftext%3E%3Ctext%20font-family%3D%22math11ce3e6e3f452828e23a0c94572%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2232.5%22%20y%3D%2216%22%3E%26%23x22A5%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2246.5%22%20y%3D%2216%22%3EB%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2258.5%22%20y%3D%2216%22%3EC%3C%2Ftext%3E%3C%2Fsvg%3E)
b/ Trên tia đối của tia AB lấy điểm E sao cho BE = BC. Gọi I là giao điểm của tia BD với CE. Chứng minh format('truetype')%3Bfont-weight%3Anormal%3Bfont-style%3Anormal%3B%7D%3C%2Fstyle%3E%3C%2Fdefs%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%225.5%22%20y%3D%2216%22%3EB%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2213.5%22%20y%3D%2216%22%3EI%3C%2Ftext%3E%3Ctext%20font-family%3D%22math11ce3e6e3f452828e23a0c94572%22%20font-size%3D%2216%22%20text-anchor%3D%22middle%22%20x%3D%2224.5%22%20y%3D%2216%22%3E%26%23x22A5%3B%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2238.5%22%20y%3D%2216%22%3EE%3C%2Ftext%3E%3Ctext%20font-family%3D%22Arial%22%20font-size%3D%2216%22%20font-style%3D%22italic%22%20text-anchor%3D%22middle%22%20x%3D%2250.5%22%20y%3D%2216%22%3EC%3C%2Ftext%3E%3C%2Fsvg%3E)
c/ Chứng minh ba điểm K, D, E thẳng hàng.
Cần gấp. Chi tiết!!!!
a: Xét ΔBAD và ΔBKD có
BA=BK
\(\widehat{ABD}=\widehat{KBD}\)
BD chung
Do đó: ΔBAD=ΔBKD
Suy ra: \(\widehat{BAD}=\widehat{BKD}=90^0\)
hay DK\(\perp\)BC
b: Xét ΔBEC có BE=BC
nên ΔBEC cân tại B
mà BI là đường phân giác
nên BI là đường cao
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối BC lấy điểm D, Trên tia đối của tia CB lấy điểm E sao cho ∠BAD = ∠CAE. Kẻ BH vuông góc với AD (H ∈ AD). kẻ CK vuông góc với AE (K ∈ AE). Chứng minh rằng : BH = CK
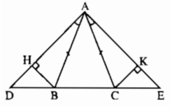
Xét tam giác BHA và ∆CKA có
∠AHB = ∠AKC = 90º
AB = AC ( vì tam giác ABC cân tại A).
∠HAB = ∠KAC ( giả thiết)
Suy ra ΔBHA = ΔCKA (cạnh huyền – góc nhọn), suy ra BH = CK.
Đúng 0
Bình luận (0)