cho tam giác ABC vuông tại A,biết AB=5Ccm,AH=3cm .tính HB,HC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A đường cao AH M là trung điểm AB, N là trung điểm AC. Tính HB, HC,AH biết HM=3cm, HN=4cm
Xét \(\Delta HAC\)vuông tại H có HN là đường trung tuyến ứng với cạnh huyền
=> HN = NC = NA = AC/2
=> AC = 2HN = 8
Tương tự AB = 6
Theo hệ thức lượng trong tam giác vuông cho tam giác ABC vuông tại A có AH là đường cao thì
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{25}{576}\)
\(\Leftrightarrow AH=\frac{24}{5}\)
Áp dụng định lí Pytago vào \(\Delta HAC\)vuông tại H có
\(HA^2+HC^2=AC^2\)
\(\Leftrightarrow\left(\frac{24}{5}\right)^2+HC^2=8^2\)
\(\Leftrightarrow HC=\frac{32}{5}\)
Tương tự \(HB=\frac{18}{5}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, AH là đường cao. Biết AB= 15cm,HC=16cm. Tính BC,AH,HB,AC
Cho tam giác ABC vuông tại A, AH là đường cao. Biết AH=12cm,AM=13cm ( AM là đường trung tuyến). Tính BC, AB,HB,AC,HC
Cho tam giác ABC vuông tại A, AH là đường cao, AD là đường phân giác. Biết AB=15cm; AC=20cm.
a. Tính AC, AH,HB,HC,BD, DC, HD, AD. b. Kẻ HI vuông góc với AB tại I, HK vuông góc với AC tại K. Chứng minh AI.AK.AC. c. Chứng minh tam giác ABC đồng dạng với tam giác AKI. d. Tính diện tích và chu vi tứ giác IBCK.a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=25-9=16cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=25/7
=>BD=75/7cm; CD=100/7cm
b: ΔAHB vuông tại H có HI là đường cao
nên AI*AB=AH^2
ΔAHC vuông tại H có HK là đường cao
nên AK*AC=AH^2
=>AI*AB=AK*AC
c: AI*AB=AK*AC
=>AI/AC=AK/AB
=>ΔAIK đồng dạng với ΔACB
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH, AB = 8, HC - HB = 8
a) Tính AC, HB, HC
b) Đường phân giác AD, tính DB, DC, AD
Cho tam giác ABC vuông tại A, AH là đường cao. BC=25cm, AH= 12cm. Tính AC, AB, HB, HC
Cho tam giác ABC vuông tại A, đường cao AH. Có AH = 2,4 cm; BC = 5 cm. Tính HB, HC, AB, AC ?
Cho tam giác ABC vuông tại A, AH là đường cao. Biết AB=15cm,HC=16cm.Tính BC,AH,HB,AC.
Đúng 0
Bình luận (0)
NHANH HỘ MÌNH VỚI !!!
Bài 5: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB:AC = 3:7, AH = 42cm. Tính HB, HC?
Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{7}\)
nên \(\dfrac{HB}{HC}=\dfrac{9}{49}\)
hay \(HB=\dfrac{9}{49}HC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{9}{49}=42^2\)
hay HC=98cm
\(\Leftrightarrow HB=\dfrac{9}{49}\cdot98=18cm\)
Đúng 1
Bình luận (0)
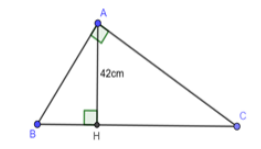
Ta có:\(\dfrac{AB}{AC}=\dfrac{3}{7}\) ⇒ AB = \(\dfrac{3}{7}\) AC
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{42^2}=\dfrac{49}{9AC^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{42^2}=\dfrac{49}{9AC^2}\)
⇔ \(AC^2=11368\Leftrightarrow AC=14\sqrt{58}\) \(\left(cm\right)\)
⇔ \(AB=\dfrac{3}{7}.14\sqrt{58}=6\sqrt{58}\) \(\left(cm\right)\)
Áp dụng định lý Pytago cho ABH vuông tại A có: \(AB^2+AC^2=BC^2\)
⇔ \(BC^2=\left(6\sqrt{58}\right)^2+\left(14\sqrt{58}\right)^2\)
⇔ \(BC^2=13456\Rightarrow BC=116\) \(cm\)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,đường cao AH biết AB = 3cm, BH = 1,8cm. Tính V, Sxq hình tạo thành khi quay tam giác vuông ABC quanh trục AB
Theo công hệ thức lương trong tam giác vuông ta có :
\(AB^2=BH.BC\Leftrightarrow9=1,8.BC\Rightarrow BC=5\left(cm\right)\)
Định lý Pytago :
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
Như vậy khi ta quay tam giác ABC quanh trục AB ta thu được hình nón có đường cao \(AB=3\) , bán kính đáy \(AC=4\) và đường sinh \(BC=5\)
Diện tích xung quanh của hình nón thu được :
\(S_{xq}=\pi rl=\pi.AC.BC=20\pi\left(cm^2\right)\)
Thể tích hình nón là :
\(V=\frac{1}{3}\pi r^2h=\frac{1}{3}.\pi.4^2.3=16\pi\) ( cm khối )














