 plss giúp vs ạ
plss giúp vs ạ

Những câu hỏi liên quan
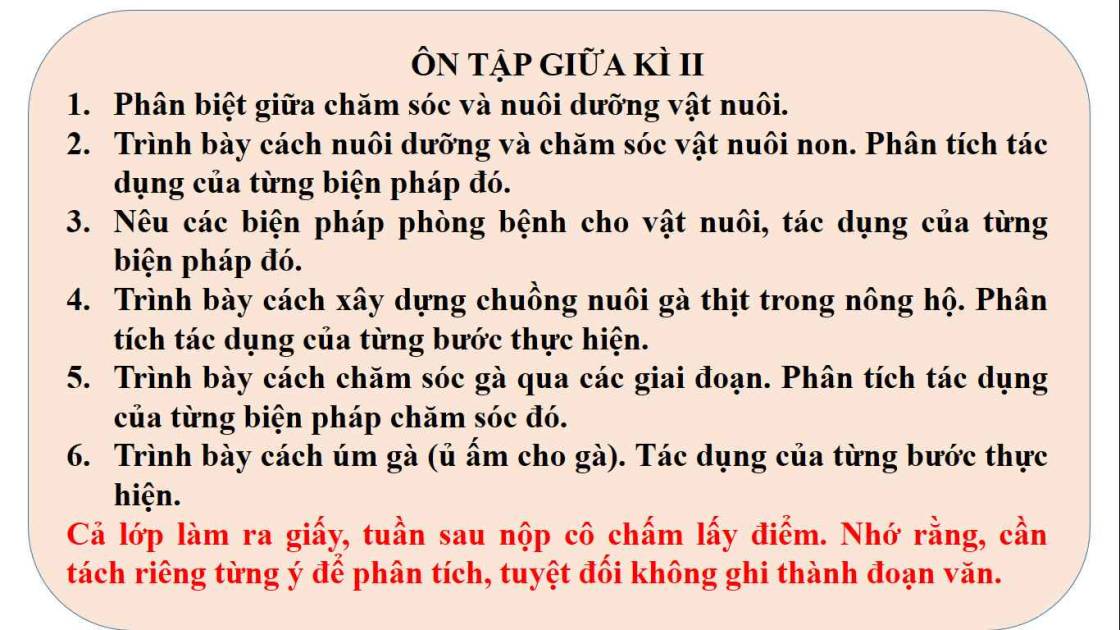
giúp vs ạ plss
giúp em 3 bài này gấp vs ạ!plss
Câu 5:
\(\left\{{}\begin{matrix}x^2+y^2=4\left('\right)\\x-y-xy=2\left(''\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2+2xy=4\\x-y-xy=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)^2+2xy=4\left(1\right)\\2\left(x-y\right)-2xy=4\left(2\right)\end{matrix}\right.\)
Lấy \(\left(1\right)+\left(2\right)\) ta được:
\(\left(x-y\right)^2+2\left(x-y\right)=8\)
\(\Leftrightarrow\left(x-y\right)^2+2\left(x-y\right)+1-9=0\)
\(\Leftrightarrow\left(x-y+1\right)^2-9=0\)
\(\Leftrightarrow\left(x-y-2\right)\left(x-y+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-y=2\\x-y=-4\end{matrix}\right.\)
Với \(x-y=2\) Thay vào \(\left(''\right)\) ta được:
\(2-xy=2\Rightarrow xy=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\Rightarrow y=-2\\y=0\Rightarrow x=2\end{matrix}\right.\)
Với \(x-y=4\Rightarrow x=4+y\) Thay vào \(\left('\right)\) ta được:
\(\left(4+y\right)^2+y^2=4\)
\(\Leftrightarrow y^2+8y+16+y^2-4=0\)
\(\Leftrightarrow2y^2+8y+12=0\)
\(\Leftrightarrow y^2+4y+6=0\)
\(\Leftrightarrow\left(y+2\right)^2+2=0\) (phương trình vô nghiệm).
Vậy hệ phương trình đã cho có nghiệm \(\left(x,y\right)\in\left\{\left(2;0\right),\left(0;-2\right)\right\}\)
Đúng 0
Bình luận (0)
Câu 6: \(\left\{{}\begin{matrix}2xy+y^2=3\left('\right)\\x^2+5xy=6\left(''\right)\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4xy+2y^2=6\left(1\right)\\x^2+5xy=6\left(2\right)\end{matrix}\right.\)
Lấy \(\left(2\right)-\left(1\right)\) ta được:
\(x^2+xy-2y^2=0\)
\(\Leftrightarrow x^2-y^2+xy-y^2=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+y\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+2y\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x=-2y\end{matrix}\right.\)
Với \(x=y\) Thay vào \(\left('\right)\) ta được:
\(2y.y+y^2=3\)
\(\Leftrightarrow y=\pm1\Rightarrow x=\pm1\).
Với \(x=-2y\) Thay vào \(\left('\right)\) ta được:
\(2.\left(-2y\right).y+y^2=3\)
\(\Leftrightarrow y^2=-1\) (phương trình vô nghiệm)
Vậy hệ phương trình đã cho có nghiệm \(\left(x,y\right)\in\left\{\left(1;1\right),\left(-1;-1\right)\right\}\)
Đúng 0
Bình luận (0)
Câu 4: \(Đk:x>-1;y>-\dfrac{1}{2}\)
Đặt \(\left\{{}\begin{matrix}a=\dfrac{1}{\sqrt{x+1}}\left(a>0\right)\\b=\dfrac{1}{\sqrt{2y+1}}\left(b>0\right)\end{matrix}\right.\)
Hệ phương trình đã cho trở thành:
\(\left\{{}\begin{matrix}2a+b=5\\3a+2b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4a+2b=10\\3a+2b=9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2a+b=5\\a=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{1}{\sqrt{x+1}}=1\\\dfrac{1}{\sqrt{2y+1}}=3\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{x+1}=1\\\sqrt{2y+1}=\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x+1=1\\2y+1=\dfrac{1}{9}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-\dfrac{4}{9}\end{matrix}\right.\left(nhận\right)\)
Đúng 0
Bình luận (0)
 mọi người cứu em ngay vs ạ plss xem đúng ko ạ
mọi người cứu em ngay vs ạ plss xem đúng ko ạ
18 A
19 A
20 B
21 C
22 A
23 D
24 B
25 C
26 B
27 B
28 C
29 C
32 A
32 B
33 B
Đúng 1
Bình luận (0)
c = -3 + -3 mũ 2 + -3 mũ 3 + ...+ -3 mũ 200 rút gọn giúp mk vs ạ:> plss
Olm chào em, em nên viết đề bài bằng công thức toán học để thầy cô, bạn bè hiểu đúng yêu cầu đề bài, em nhé. Có như vậy mọi người mới trợ giúp em được tốt nhất. Cảm ơn em đã đồng hành cùng Olm.
Đúng 0
Bình luận (0)
Ta có: \(C=\left(-3\right)+\left(-3\right)^2+\left(-3\right)^3+\cdots+\left(-3\right)^{200}\)
=>\(\left(-3\right)C=\left(-3\right)^2+\left(-3\right)^3+\left(-3\right)^4+\cdots+\left(-3\right)^{201}\)
=>\(-3C-C=\left(-3\right)^2+\left(-3\right)^3+\cdots+\left(-3\right)^{201}-\left(-3\right)-\left(-3\right)^2-\cdots-\left(-3\right)^{200}\)
=>\(-4C=\left(-3\right)^{201}-\left(-3\right)=-3^{201}+3\)
=>\(4C=3^{201}-3\)
=>\(C=\frac{3^{201}-3}{4}\)
Đúng 0
Bình luận (0)
Giúp mik vs plss
Giúp mik câu 5 vs, plss

 giúp em với ạ plss
giúp em với ạ plss
1: Ta có: AG=2/3AD
GM=GD+DM=2GD=2/3AD
Do đó: AG=GM
hay G là trung điểm của AM
3: Xét tứ giác BGCM có
D là trung điểm của BC
D là trung điểm của GM
Do đó: BGCM là hình bình hành
Suy ra: BG=CM
Đúng 0
Bình luận (0)

mn ơi giúp mik bào này dc ko ạ plss mn ạ
1: AD=8-2=6cm
AD/AB=6/8=3/4
AE/AC=9/12=3/4
=>AD/AB=AE/AC
2: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc A chung
=>ΔADE đồng dạng với ΔABC
3: AI là phân giác
=>IB/IC=AB/AC
=>IB/IC=AD/AE
=>IB*AE=AD*IC
Đúng 0
Bình luận (0)
Mọi người giải giúp mik với ạ, plss 🥺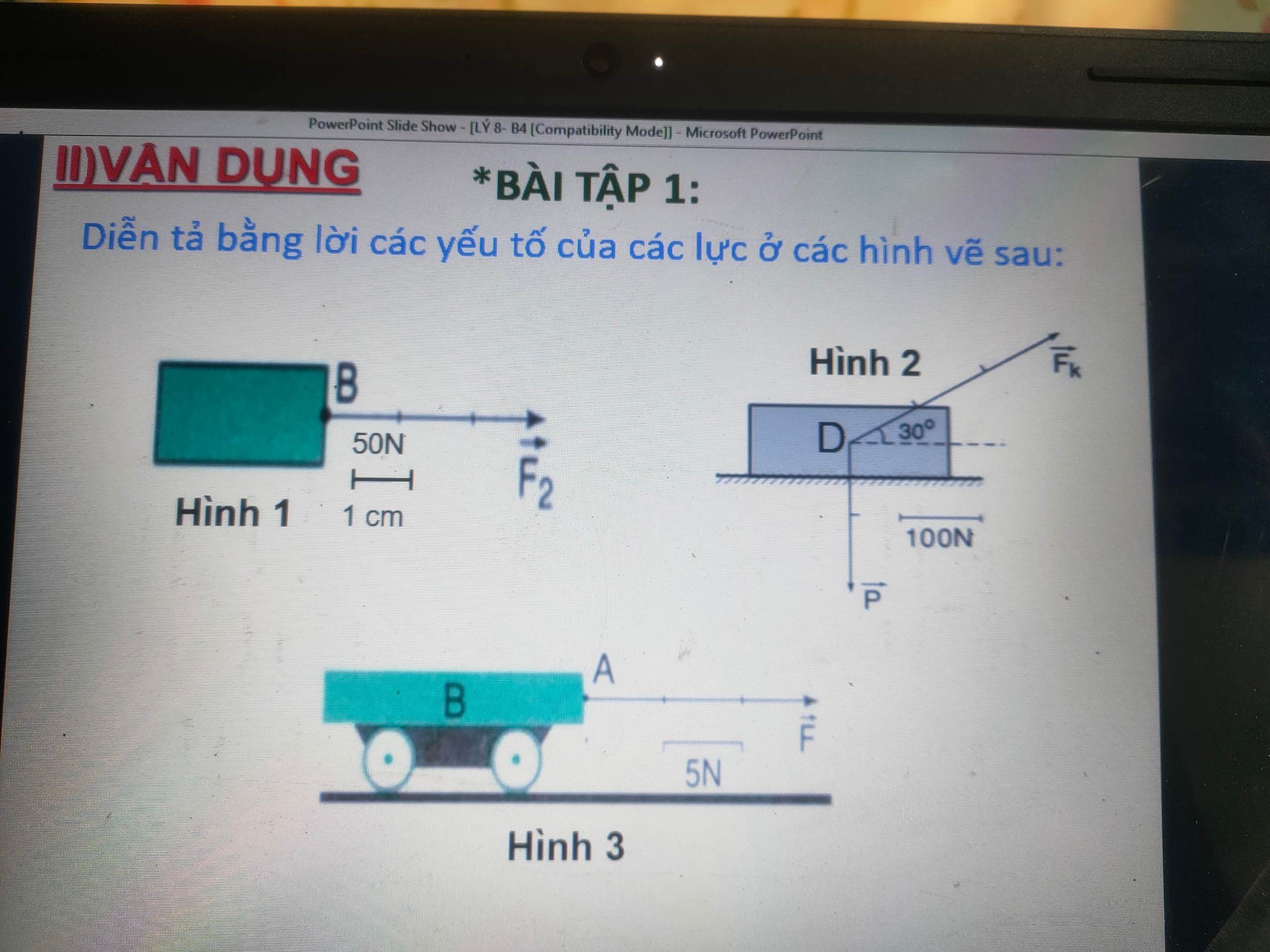

Giúp mình với plss mình cần gấp lắm ạ :((
a: \(VT=\left(\dfrac{\sqrt{7}\left(\sqrt{2}-1\right)}{2\left(\sqrt{2}-1\right)}+\dfrac{\sqrt{5}\left(\sqrt{3}-1\right)}{2\left(\sqrt{3}-1\right)}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)\)
\(=\left(\dfrac{\sqrt{7}+\sqrt{5}}{2}\right)\cdot\left(\sqrt{7}-\sqrt{5}\right)=\dfrac{7-5}{2}=\dfrac{2}{2}=1\)
=VP
b: \(VT=3-\sqrt{5}+2\left(\sqrt{5}+1\right)-\left|\sqrt{5}-2\right|\)
=3-căn 5+2căn 5+2-căn 5+2
=3+2+2=7
=VP
Đúng 2
Bình luận (1)
















