Với \(z\) là ẩn; \(m\), \(n\), \(p\) là các số và \(m\ne-n;n\ne-p;p\ne-m\).
Giải phương trình: \(\dfrac{z-mn}{m+n}+\dfrac{z-np}{n+p}+\dfrac{z-pm}{p+m}=m+n+p\)
Số nghiệm của phương trình với ẩn số phức z: 4z2 + 8|z|2 - 3 = 0 là:
A. 3.
B. 2.
C. 4.
D. 1.
Chọn C.
Gọi z = a + bi là nghiệm của phương trình.
Ta có: 4(a + bi) 2 + 8(a2 + b2) - 3 = 0
4(a2 – b2 + 2abi) + 8( a2 + b2) - 3 = 0
12a2 + 4b2 +8abi - 3 = 0
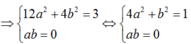
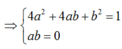

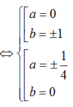
Vậy phương trình có 4 nghiệm phức.
Giải hệ phương trình
\(\left\{{}\begin{matrix}-2x+y+z=a\\x-2y+z=b\\x+y-2z=c\end{matrix}\right.\) với x,y,z là các ẩn số
\(\Leftrightarrow\left\{{}\begin{matrix}3x-3y=b-a\\3x-3y=2b+c\\x+y-2z=c\end{matrix}\right.\) (nhân -1 vào 2 vế pt 1 và cộng pt 2, nhân 2 vào 2 vế pt 2 và cộng pt 3)
\(\Leftrightarrow\left\{{}\begin{matrix}0=a+b+c\\x-y=\dfrac{2b+c}{3}\\x+y-2z=c\end{matrix}\right.\)
- Nếu \(a+b+c\ne0\) hệ vô nghiệm
- Nếu \(a+b+c=0\) hệ có vô số nghiệm
Giải hệ phương trình
\(\left\{{}\begin{matrix}-2x+y+z=a\\x-2y+z=b\\x+y-2z=c\end{matrix}\right.\) với x,y,z là các ẩn số
Cho a , b , c ∈ R ; a ≠ 0 ; b 2 - 4 a c < 0 . Tìm số nghiệm phức của phương trình a z 2 + b z + c = 0 (với ẩn là z)
A. 3
B. 2
C. 1
D. 0
Kí hiệu n là số các giá trị của tham số a sao cho phương trình z 2 + a z + 3 = 0 ( với ẩn là z ), có hai nghiệm phức z 1 ; z 2 thỏa mãn z 1 2 + z 2 2 = - 5 . Tìm n.
A. n = 0
B. n = 1
C. n = 2
D. n = 3
Câu 1: Cho ví dụ về phươg trình
- với ẩn là x
- với ẩn là t
- với ẩn là m
vd với ẩn x: 2x+3=0
với ẩn t: t+11=0
với ẩn m: 5m+15=0
1.nêu điểm gióng và khác giữa so sánh và ẩn dụ, ẩn dụ với hoán dụ, bạn nào cho mik biết đề tập làm văn năm nay hok,mấy bạn ôn tả gì z? help nhá
so sánh là đối chiếu sự vật này vs sự vật kia, ẩn dụ là gọi tên sự vật này vs sự vật kia
ẩn dụ là tương đồng , hoán dụ là tương cận( quan hệ gần gũi)
trường mình hình như là tả người hc tả cảnh còn trường bn thì mình ko bt
Cho ba số thực x,y,z .Đặt a=x+y+z,b=xy+yz+zx,c=xyz.
Chung minh cac pt sau đều có nghiệm
X^2+2aX+3b=0
aX^2-2bX+3c=0
Với X là ẩn.
Xét phương trình thứ nhất:
X2 + 2aX + 3b = 0
Ta có: ∆' = a2 - 3b
= (x + y + z) 2 - 3(xy + yz + zx)
= x2 + y2 + z2 - xy - yz - zx
\(\frac{\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2}{2}\ge0\)
Vậy PT X2 + 2aX + 3b = 0 có nghiệm với mọi x, y, z.
Phương trình còn lại làm tương tự nhé.
Giải hệ phương trình với các ẩn số x,y,z sau đây
\(\frac{xz}{ax+by}=\frac{yz}{bz+cy}=\frac{zx}{cx+az}=\frac{x^2+y^2+z^2^{ }}{a^2+b^2+c^2}\)
với a,b,c là các số cho trước