Cho tam giác ABC vuông cân tại A, M là 1 điểm trên cạnh BC.C/M: MB2+MC2 = 2MA2

Những câu hỏi liên quan
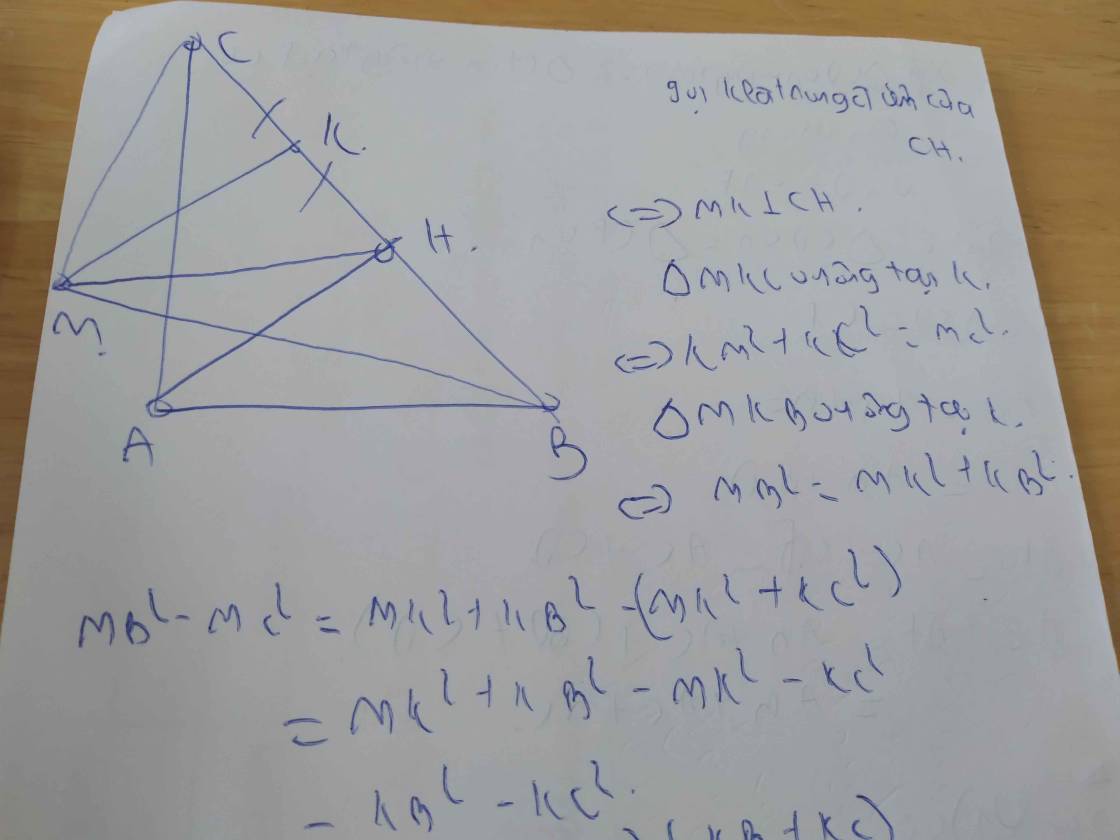
Cho tam giác ABC vuông tại A có AB<AC. Đường cao AH, AB = 4cm. Gọi M là điểm bất kì trên đường
trung trực của HC. Tính MB2 - MC2
Tam giác abc cân tại a có góc a=80 độ . Trên cạnh bc lấy điểm d,e sao cho bd=ce<1/2 bc
A. Tính số đo của góc b. Góc c của tam giác abc
B.c/m tam giác ade cân
C kẻ dh vuông góc ab, ek vuông góc với ac( h€ab,k€ac).c/m ah=ak
D. Gọi m là trung điểm của bc.c/m 3 đường thẳng am, dh, ek cắt nhau tại 1 điểm
Cho tam giác ABC vuông cân tại B và M thuộc miền trong tam giác sao cho góc BMC =135 độ. Chứng minh MA2=2.MB2+MC2
Cho tam giác ABC vuông cân tại A, M là 1 điểm trên cạnh BC.C/M: MB2+MC2 = 2MA2
Cho tam giác đều ABC cạnh a.
a, Cho M là một điểm trên đường tròn ngoại tiếp tam giác ABC. Tính MA2 + MB2 + MC2 theo a.
b, Cho đường thẳng d tùy ý, tìm điểm N trên đường thẳng d sao cho NA2 + NB2 + NC2 nhỏ nhất.
a) Gọi O là tâm đường tròn ngoại tiếp. Do tam giác ABC là tam giác đều nên O đồng thời là trọng tâm tam giác đều ABC.
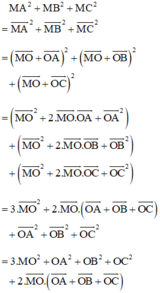
Lại có:
+ O là trọng tâm tam giác nên 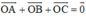
+ Bán kính đường tròn ngoại tiếp tam giác:
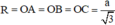
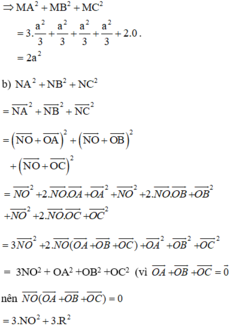
Ta có: NA2 + NB2 + NC2 ngắn nhất
⇔ NO2 ngắn nhất vì R không đổi
⇔ NO ngắn nhất
⇔ N là hình chiếu của O trên d.
Đúng 0
Bình luận (0)
cho tam giác abc vuông tại a (AB<AC) trung tuyết AM, Trên AM lấy D sao cho m là trung điểm của AD a) c/m tứ giác ABDX là hcn b) vẽ E dối xứng qua BC.C/M AE vuông góc ED c)c/m tư giác BCDE là hình thang cân
a: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Đúng 0
Bình luận (1)
cho tam giác abc cân tại a. Trên cạnh bc lấy điểm d sao cho bd=1/3 bc.c/m bad=1/3bac
Cho tam giác ABC .Ngoài tam giác ABC vẽ các tam giác ABE vuông cân tại B, tam giác ACF vuông cân tại C.Vẽ Bx //AC,Cy//AB cắt nhau tại D
1.C/m góc ABD=gócDCF
2.M là giao điểm của AD và BC.C/m M là trung điểm của AD
3.
Cho tam giác ABC vuông tại A góc b bằng 60 độ tia phân giác c cắt AB tại m. Từ m kẻ MH vuông góc với BC cắt tia CA tại k. Gọi n là điểm BC.C/M
A, MH=MA
B, tam giác MHB= MAK
C,tam giác BCA cân
D,tam giác ABN là tam giác đều
Cho tam giác ABC vuông cân tại A. Gọi E là trung điểm của BC. M là điểm bất kì thuộc cạnh BC (M khác E). Kẻ BH vuông góc với AM tại H và CK vuông góc với AM tại K.
a) Chứng minh △KAC = △HBA
b) Chứng minh AE vuông góc với BC.
c) Tam giác KEH là tam giác gì? Vì sao?
b: Ta có: ΔABC cân tại A
mà AE là đường trung tuyến
nên AE là đường cao
Đúng 0
Bình luận (0)